0

Introduction

For a long time I have struggled with (the idea of) password management. Remembering unique strong passwords is impossible when one has more than a handful, which only leaves the option of using a password management system of some sort. The conventional backed-up randomly generated passwords never appealed to me, as it gets increasingly difficult to update your database of passwords with every back-up copy—and I would demand a lot of them (I refuse to ever lose my passwords).

Naturally I became interested in deterministic password-generation algorithms and I carelessly and stubbornly searched for an answer, to no avail. Time passed, and as I—on an unrelated journey—got familiar with the crypto-currency technology, the final puzzle started to fall into place. I formulated a password generator that doesn't need any back-ups, but it has not been scrutinized by anyone, let alone security experts. Hence, this is my plea and question to you: Is there a flaw or are we ready to revolutionize password management?

I will present the idea in two parts. Firstly, an explanation of the crucial obfuscation process—the final piece of the puzzle— that was inspired by Bitcoin's standard to safely store keys.

Part one: the obfuscation process

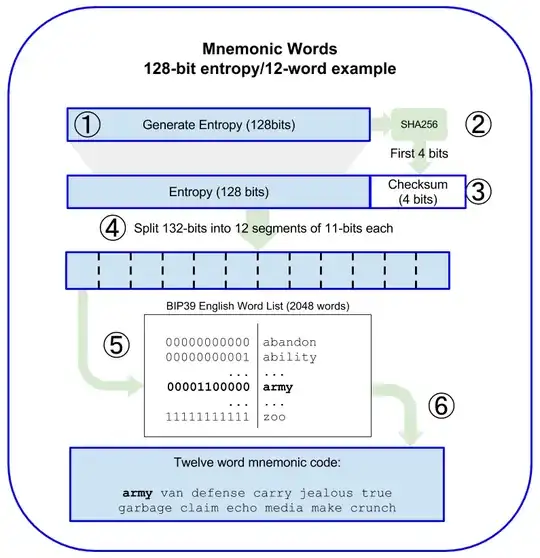
This wordlist of 2048 words is widely used in the crypto-currency space. It is used by taking a hash, appending to it a checksum sliced to the length of [entropy/32] in order to make it divisible by 11, and dividing it into segments of 11 bits—each segment corresponding to one of the words in the list (00000000000 would be the first word—"abandon", and 11111111111 would be the last word—"zoo"). Thus the hash is converted into a string of human-readable words.

Here is an infographic from Mastering Bitcoin that illustrates this:

enter image description here

Example:

Password:

"CorrectHorseBatteryStaple"

SHA-256 sum:

7abdae32d3c9fd31959fd66c8c48de11bdff24b1dad2542f46faa0ebc50329fe

(01111010 10111101 10101110 00110010 11010011 11001001 11111101 
00110001 10010101 10011111 11010110 01101100 10001100 01001000 
11011110 00010001 10111101 11111111 00100100 10110001 11011010 
11010010 01010100 00101111 01000110 11111010 10100000 11101011 
11000101 00000011 00101001 11111110)

SHA-256 sum with check:

7abdae32d3c9fd31959fd66c8c48de11bdff24b1dad2542f46faa0ebc50329fe5b

(01111010 10111101 10101110 00110010 11010011 11001001 11111101 
00110001 10010101 10011111 11010110 01101100 10001100 01001000 
11011110 00010001 10111101 11111111 00100100 10110001 11011010 
11010010 01010100 00101111 01000110 11111010 10100000 11101011 
11000101 00000011 00101001 11111110 01011011)

SHA-256 sum with check split into segments of 11 bits:

  • 01111010101 (981 - "kind")
  • 11101101011 (1899 - "unhappy")
  • 10001100101 (1125 - "milk")
  • 10100111100 (1340 - "polar")
  • 10011111110 (1278 - "panic")
  • 10011000110 (1222 - "obvious")
  • 01010110011 (691 - "film")
  • 11111010110 (2006 - "wide")
  • 01101100100 (868 - "hockey")
  • 01100010010 (786 - "giraffe")
  • 00110111100 (444 - "danger")
  • 00100011011 (283 - "cash")
  • 11011111111 (1791 - "thank")
  • 10010010010 (1170 - "mutual")
  • 11000111011 (1595 - "shrug")
  • 01011010010 (722 - "focus")
  • 01010100001 (673 - "favorite")
  • 01111010001 (977 - "key")
  • 10111110101 (1525 - "salon")
  • 01000001110 (526 - "double")
  • 10111100010 (1506 - "rotate")
  • 10000001100 (1036 - "lift")
  • 10100111111 (1343 - "pond")
  • 11001011011 (1627 - "slender")

We don't need all 24 words. Taking the first 7 words we get 2048^7 > 10^23 possible passwords. That should be enough entropy.

Obfuscated password:

"KindUnhappyMilkPolarPanicObviousFilm"

This allows us to generate human-readable hashes of our passwords, which means that our passwords can be extremely similar to each other, because we will keep them secret and use their obfuscated forms instead.

Part two: the complete system

The idea is to have one strong master password for the rest of your life that works as a salt. A new password is generated by appending a name (presumably of the website) together with an integer (for multiple passwords on the same website) to the master password before it is obfuscated to create the password.

Let's assume our master password is "CorrectHorseBatteryStaple".

I wish to create a new account on StackExchange and decide to generate a password for it:

  1. The password manager asks for a name and number (default: 1) for the password. I type "StackExchange" and change the number to 2, as this would be my second StackExchange account.

  2. The password manager turns the name into lower case, and appends it and the number to the master password: "CorrectHorseBatteryStaplestackexchange2"

  3. The password manager obfuscates the string and presents the obfuscated password for my new StackExchange account to me: "ParentTinyGiftCenturyCurveBlessInput"

The password manager can save these passwords, but it is unnecessary. Whenever I want to log in to my second StackExchange account I can simply write "stackexchange" and "2" in the two fields in order to be presented with my password.

There are a few obstacles that need to be tackled. Many websites have silly restrictions on passwords such as a maximum password length of 20 and requiring non-alphanumberic characters. These problems could be bypassed by simply ending every password with an asterisk and allowing for 4-word passwords in addition to the standard 7-word password. However, I am unsure about whether it is the correct approach to include these hacks, as this should be a widely adopted standard rather than merely used by a small minority of enthusiasts.

Adoption is important to reduce fingerprintability. I am currently using this technique for my passwords, but since I am the only person on the planet who uses it, I cannot use it when I want to be anonymous. That is a major problem, but one that eventually goes away if this turns out to be as widely adopted as I think it deserves to be.

Compared to conventional password managers, this is—as I can see—more secure and incredibly more convenient (which plays a major role in adoption).

Update: I am not exactly sure why this is off-topic, but in any case I realize that my idea is infeasible after reading the comments and reflecting over them. This question may now be closed.

Community
  • 1
Gendarme
  • 199
  • 5
  • 2
    As a first step think like an attacker. It is up to the inventor of a new method to do the research, there is no reason to believe knowable crypto experts will take their time to review such a scheme without serious literature review by the author. Obfuscated is insufficient. Obligatory: ["Schneier's Law"](https://www.schneier.com/blog/archives/2011/04/schneiers_law.html): "*Anyone, from the most clueless amateur to the best cryptographer, can create an algorithm that he himself can't break.*" – zaph Jan 09 '19 at 01:04
  • You haven't mentioned current best practices such as Argon2 which require substantial time and/or memory. You must show that your menthod is at lease as secure. Review and compare to [NIST Digital Identity Guidelines](http://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-63b.pdf) (unfortunately not currently available). Show that this scheme to not vulnerable to [rainbow table](https://en.wikipedia.org/wiki/Rainbow_table) attacks, etc. – zaph Jan 09 '19 at 01:20
  • 3
    Before coming up with a solution to an existing problem, you need to first consider *how existing approaches fall short*. Otherwise, you end up inventing solutions to problems that don't exist. That seems to be the case here. – Stephen Touset Jan 09 '19 at 01:56
  • 2
    Voted to close as primarily opinion-based/off-topic because security.SE should not be used to audit home-grown algorithms. Even for ones that has gained traction they should go to https://crypto.stackexchange.com, not here. – Voile Jan 09 '19 at 03:07
  • `...or are we ready to revolutionize password management?` Probably, the next revolution is finally going to _remove_ passwords, in preference for some sort of distributed id. Something like, say, [an "internet driver's license"](https://blog.codinghorror.com/your-internet-drivers-license/). Remember that passwords are absolutely **not** a goal - they're a necessary part of a solution. The actual goal is proving your identity to a requestor. – Clockwork-Muse Jan 09 '19 at 05:44
  • @StephenTouset I thought I did. In my view they fall short as it is practically impossible to keep your password vault redundantly backed-up while still being able to add new passwords. – Gendarme Jan 09 '19 at 08:14
  • I'll write a comment because this is now on hold. Here's why your solution isn't good, the cons: 1) All the passwords are related to each other: they are all generated by a specific algo, and the only unknown parameter is the master password. So by knowing your Google password, if I manage to bruteforce it and get your master password I can then know ALL your other passwords; 2) If you just need to change your master password (for example because you suspect somebody has been shoulder surfing), that will generate different passwords and you will have to go change ALL of them. To be continued. – reed Jan 09 '19 at 10:54
  • Continuing with the cons: 3) Your method makes it difficult to change a single password. You would end up having Google1, Google2, Google3, etc. and you would have to remember (store) the number, which will change every time you need to change or reset a password. 4) Your method doesn't allow specific passwords that you can't control: passwords that must be in a certain form (numeric PINs, etc.) and other people's passwords that you might need to manage: your parent's, your client's, etc. For all these reasons I would not use your method. – reed Jan 09 '19 at 11:02
  • I'm interested in new methods for password management too, but for a different reason than yours. I'd like to solve the problem of the "single point of failure", which causes ALL the passwords to be stolen if your machine was infected with specific malware. I've only come up with a solution so far, but I still have to perfect it and define the details. Also, unlike you, I don't consider backups to be a problem, so I don't think your solution solves a real problem for me. – reed Jan 09 '19 at 11:10
  • @reed You can't (unless you break SHA-2) reverse engineer the obfuscated password, but I see your point. I didn't realize that the single point of failure of the master password would be a liability to this extent. Clearly my idea is infeasible. I think I will simply keep an AES-encrypted text-file with my most important passwords and keys, and store all less important passwords in a conventional PW-manager with only a few back-ups. Please share your solution regarding the single point of failure; I am very curious. – Gendarme Jan 09 '19 at 17:13
  • @Gendarme Backing up doesn't seem particularly difficult. I have a 1Password vault that's simultaneously synced between my phone, laptop and an iCloud account, and I have on-site backups that happen regularly. None of this was particularly difficult to set up, and is easily within the reach of most non-technical people. Passwords are read significantly more frequently than they're written, so keeping these devices in sync is mostly trivial from a user-facing perspective since sync conflicts are practically non-existent. – Stephen Touset Jan 09 '19 at 19:22
  • Password managements based around this idea (though with more robust crypto) had been around for some time: https://lesspass.com/. The main problem with this idea is that you practically really still need a database to keep track of all those site-specific settings and site counters. Also, the other problem with this scheme is that it really just attacks password management at its strongest point: encryption. The encryption is really one of the easier part of a password manager to implement, secure autofill and domain checking is where things gets really difficult. – Lie Ryan Jan 22 '19 at 10:28

1 Answers1

7

This is a lot of trouble to go to for little additional benefit - compared with simply using a strong, random master passphrase, coupled with 2FA, to protect a password vault (within which each password can be completely random, and unrelated to both your master password and to all of your other passwords).

If the attacker somehow discovers your scheme, and if they learn your master password via any means at all, they can determine your password on all websites. And unlike using a master password for a password vault, they don't have to compromise your computer or your vault provider, or to even log into your vault provider, to use them.

Royce Williams
  • 9,318
  • 1
  • 32
  • 55
  • CRYPTO-GRAM,October 15, 2017, by Bruce Schneier: ... use password managers ... – zaph Jan 09 '19 at 02:25
  • Are you saying that one should not back up their password vault or that updating back-ups of one's password vault requires little trouble? I don't see how either of those statements is true. I did say that I find password management incredibly difficult, so it's not "little additional benefit" as I see it. What am I missing? – Gendarme Jan 09 '19 at 08:11
  • @Gendarme 1: Security it a PITA, get used to it. 2: Decide on a per-site basis the security and the level you need. Examples are a bank account vs a site where you don't care. 3: Backup can be easy with services such as Backblaze, iCloud, Time Machine, etc. I'm the paranoid type so I have on-site backups that run every hour and others that run every day but that is overkill. 4. For passwords periodically print them out and put that list in a secure (not fireproof) safe, possibly at your bank. Cheap flash drives are also good but put then in individual large labeled envelopes to prevent loss. – zaph Jan 09 '19 at 13:06
  • @Gendarme, all I meant is that your proposed method is significantly less secure than what I outlined in my first paragraph, for the reasons outlined in the second paragraph. The more deterministic a scheme is, once your methodology is known, it can be more easily compromised - which is less compliant with Kerkhoff's principle. I see that you're trying to trade a little security for more usability, but you're sacrificing more security than may be apparent. – Royce Williams Jan 09 '19 at 23:51