Approximately how much entropy in each of these low entropy sources?

Question

We need a lot of entropy. Let's be a little unrealistic and assume that we don't have access to entropy pools like dev/random, and must do all the entropy collection ourselves. The program is running on a user's computer, but they may not allow us to access some hardware that could act as entropy sources (a camera, microphone, etc would provide lots of entropy almost instantly).

These are the ones I thought of. They should commonly be available on all platforms. If there's any other good sources do point them out, but I only want a realistic estimate to the amount of entropy in each of these.

These aren't just low entropy sources, the data points are related and so N of the same type will provide much less than N times the entropy. An estimate for N of them would be good too.

• The current time. At worst we have a low precision time like seconds or milliseconds, at best we get nanoseconds or a cycle counter. The good thing about this is we can fetch the time multiple times, every time an event fires during the entropy generation process we can take the time. We could also take the time again after doing some work like haveged does.
• A pointer. We can create a dummy object and take the pointer as a value. Memory locations in the heap are generally unique, and a more complex program with more objects will result in more entropy for a pointer. With more objects there is the risk of related pointers, with the worst case being that a big chunk of memory is allocated for the N objects and so we have no more entropy than 1 object.
• Mouse clicks and movement. The cursor location mirrors the user's hand movement, which is quite smooth, so while a single mouse event has very little entropy, many mouse events over some time period can have decent entropy. It may be better then to measure by time passed rather than number of mouse events.
• Key pressed or released. Best case scenario, the user "randomly" mashes the whole keyboard. Worst case scenario, a small set of buttons are pressed in a somewhat predictable order. A likely and reliable case is typing - we can tell the user to "type anything" and instead measure by entropy per character.

Feeding from other programs, files or network stuff will vary for each case so I'm not considering them here.

---

This is just theoretical stuff. Of course I'm going to use dev/urandom when it's available and not need to worry about collecting entropy myself.

Also, coming up with a number (or formula for N) for each of these may be a difficult problem in and of itself. I would still like a rough estimate for all of them, but the pointers one seems to be the least studied and is the one I'm most interested in.

I would like the estimate to be realistic rather than undershooting, since with an accurate estimate we can properly tune the security margin.

---

Edit 1 - Mouse movement (20 Oct.)

Just to clarify what I mean by realistic, the future attacker we are worried about will use the best method available to reduce the entropy, but this method is not magic. Thus we should try to model our entropy source multiple ways, calculate an entropy estimate for each of them, and use the minimum of those to derive our final "realistic" estimate.

Mouse movement models a person's hand moving, and that movement will be smooth. It's measured in pixels at irregular intervals though. For my model I break this up into the acceleration, being the original movement and measured per second, and the noise, being the byproduct of reading the movement and measured per event.

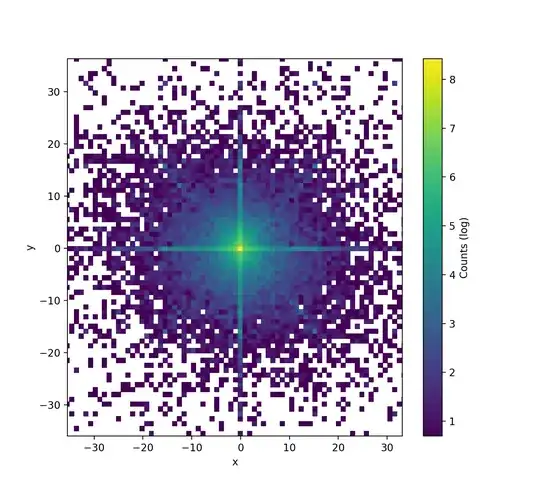
Acceleration histogram looks like this up close:

Very bright center is due to there being exponentially more slow movement than fast movement. Bright axes are from horizontal and vertical movement. Somewhat bright diagonals I think are from transitioning between horizontal and vertical movement.

A lot of other things follow a normal distribution. Mouse movement not quite but it's very close. Some curve fitting and parameter testing later and we end up with 79.4 bits/second from acceleration plus 0.33 bits/event from noise, which for my rates result in an average 3.07 bits of entropy per event.

This was measured from a toy meant to simulate real mouse usage. Jittering would be much higher entropy due to the speed of the mouse moving and the frequency of direction changes, and is probably what would happen if we told the user to move their mouse around. 2 seconds of mouse movement meets 128-bit security with a large margin, and 4 seconds gets 256-bit. Assuming there's no keyloggers or the like to compromise that entropy source anyway.

I probably won't get around to making a model for the pointers, since memory allocation isn't really standardized.

Note: this is only with the constants I chose and my mouse movement. Yours will be different. Probably not so different though. As for monitor/window size, because I used a normal-ish distribution, the edges wouldn't contribute much anyways. The noise will definitely change, but unless you have an unusually slow mouse the acceleration will still contribute a certain minimum amount of entropy per second. There is a trade-off with larger acceleration buckets (lower entropy) for more noise (more entropy), but my model is a little too simple for that.

Note 2: all models I tried didn't really fit the data. The numbers here come from the canonical normal distribution, which though it was the worst fit, gave a very low entropy of 3.07 bits/event. Second place for entropy minimum was a polynomial-based curve at 8.69 bits/event, and the best fit goes to a mixed normal-like distribution at 9.62 bits/event.

Answer 1

I cannot provide in bits exactly how much entropy can be collected from each of the sources you provide, but I can explain how they work and how effective they are relative to each other. A common conservative estimate (I know you didn't want one) would be that each unpredictable event will contain at least one bit of entropy. There is no way to actually provide a real number.

You may want to look at drivers/char/random.c from the Linux kernel to see how it collects entropy from sources such as mouse movements and keystrokes.

---

The current time. At worst we have a low precision time like seconds or milliseconds, at best we get nanoseconds or a cycle counter. The good thing about this is we can fetch the time multiple times, every time an event fires during the entropy generation process we can take the time. We could also take the time again after doing some work like haveged does.

This is a component of nearly all modern randomness sources. However, what is important is not simply measuring time, but knowing when to do the measurement. You can't just measure at fixed intervals, because then there will be a correlation between the sampled time. You can't measure only once at boot and once at shutdown, because then too little entropy is gathered. Instead, you have to measure the time whenever an unpredictable event occurs.

A pointer. We can create a dummy object and take the pointer as a value. Memory locations in the heap are generally unique, and a more complex program with more objects will result in more entropy for a pointer. With more objects there is the risk of related pointers, with the worst case being that a big chunk of memory is allocated for the N objects and so we have no more entropy than 1 object.

This is completely ineffective. Memory locations are extremely predictable, and both the behavior of the stack and memory allocators are not designed for randomness. Even in the case where the pointer has a random offset, such as when ASLR is in use, you would simply be getting the entropy from the system (RDRAND for modern Linux systems using ASLR) in a very roundabout way.

Mouse clicks and movement. The cursor location mirrors the user's hand movement, which is quite smooth, so while a single mouse event has very little entropy, many mouse events over some time period can have decent entropy. It may be better then to measure by time passed rather than number of mouse events.

This is actually a very good source of entropy, but only if the precise time in nanoseconds of each mouse event is sampled, not only the sample value itself. Even more entropy can be sampled if a PS/2 mouse is in use, as those do not use discrete sampling at a fixed sample rate but instead are interrupt driven. That is, whenever the mouse is moved, an interrupt fires which stops the CPU doing whatever it is doing and causes it to execute an interrupt handler. This handler not only reads the value being sent from the mouse, but also records the exact current time. Linux specifically takes both software ticks (jiffies) and the current cycle count.

Key pressed or released. Best case scenario, the user "randomly" mashes the whole keyboard. Worst case scenario, a small set of buttons are pressed in a somewhat predictable order. A likely and reliable case is typing - we can tell the user to "type anything" and instead measure by entropy per character.

A keyboard acts identically to a mouse as an entropy source. This entropy does not come from someone consciously bashing on the keyboard, but from the intrinsic stochastic behavior of our motor neurons. While we may be typing at a fairly regular interval, there is a huge amount of unpredictable timing delay in the microsecond and nanosecond range introduced by our naturally inaccurate neurons. This is where entropy from a HID comes from.