When choosing a numeric PIN, does it help or hurt to make each digit unique?

Question

Imagine a typical 4-digit PIN scheme containing the digits [0-9]. If I choose my PIN at random, I will get one out of 10 * 10 * 10 * 10 = 10,000 codes. Based on my own experience, more than half of the time a random sequence of four digits will contain some property or pattern that significantly lowers its entropy: single digit used in more than one position, ascending/descending pattern, etc. (Yes, yes, a 4-digit PIN only has something like 13 bits of entropy max to begin with, but some random codes are even more awful.)

If I were abide by a rule where I only use a PIN that has a unique digit in each position, I believe the number of codes available to me becomes 10 * 9 * 8 * 7 = 5,040 (somebody please correct me if I got that wrong). I have almost halved my key space, but I have also eliminated many of the lower-entropy codes from consideration.

At the end of the day, did I help or hurt myself by doing that?

EDIT: Wow, lots of great responses in here. As a point of clarification, I was originally thinking less in terms of an ATM/bank PIN (which likely has an aggressive lockout policy after a number of incorrect guesses) and more in terms of other "unsupervised" PIN-coded devices: programmable door locks, alarm system panels, garage door keypads, etc.

Answer 1

The thing is, with a 4 digit pin, entropy isn't really important. What's important it the lockout and the psychology of the attacker.

The keyspace is so small that any automated attack (without lockout) would exhaust it almost instantly.

What you're worried about is an attacker guessing the pin before the account locks. So assuming a sane lockout (say 3-5 incorrect attempts), you want your PIN to be outside the 3-5 most likely to be chosen PINs.

Personally I'd avoid any 4 digit repeating sequence and anything starting 19XX which would be a year of birth.

Now smart alecs will say "ahh but if you do that the attackers will know not to try those", but that only applies if a) the majority of the user population follow that advice (hint, they probably won't) and b) the attackers know that the user population has followed that advice.

Some great analysis of this (link courtesy of @codesincahaos)

Edit 2 - For a far more mathematical take on this I'd recommend reading @diagprov's answer

Answer 2

I'm going to barge in and talk about entropy and probability for a little bit and hopefully this will help you understand.

Firstly what is probability? This is actually an open question amongst statisticians but here's the frequentialist definition: we say that if a fair coin is flipped, it has probability 0.5 of coming up heads. However, if you flip a coin you might observe that the first five results are all heads, which does not look right. So, the frequentialist says that if you were to flip the coin "enough" times, you would eventually find that one in two of the coin tosses are heads.

The key is that probability says nothing about what will actually happen. A high-entropy password could be guessed on the very first try by simple luck, regardless of possible outcomes and so on.

Now what is entropy? If you started saying "well it's the number of possible outcomes..." you might be right in a generating-some-random-data context, but this is the perfect example of where you really need to understand what is going on underneath.

Firstly, let's talk about self-information. This is a random variable (which means there are a number of possible outcomes) that varies over the probability of each outcome (and then we take -log2(P(X)) to encode it into "bits" of information). So we need to assign each outcome a probability.

As others have pointed out, some variations of PIN choice are more likely. All the same numbers (1111, 2222, 3333, ...), Birthdays (20XX, 19XX) and so on. You should assign higher probability to these numbers because simply put people are more likely to pick them and are certainly not going to pick a random sequence. How you assign probability to other numbers is entirely up to you and really depends on how much you know about the process of choosing a pin.

Now, entropy, or to keep @codesinchaos happy, Shannon entropy specifically, is the mean of the self information distribution. It's the "most likely" value of self-information given the probabilities of each choice. What does this mean? As the current top-voted answer says, it is a measure of the choice process and how good it is, not the pin itself.

What happens when you take out high probability choices like 1111, 2222, 3333? These outcomes give very low self information (-log(P(X)) is small for large probabilities, since we expect them to occur) and so removing them moves the distribution to the right, i.e., moves the location of the distribution towards the centre. This will increase its mean. So, removing choices most people would otherwise make with high probability actually increases entropy.

Let's look at entropy in a different way: if you were going to guess PINs, in what order would you try them (assuming no lockout)? You would begin with the most likely PINs for certain. What entropy is saying is that if you repeated this experiment enough times (i.e. tried to guess the PIN of a large number of cards whose PINs were chosen with the exact same logic) then a lower entropy choice would give you, the attacker, success more quickly.

Again, this remains a question of what might happen in the theoretical case of many cards, not what might happen because the attacker gets lucky.

Here is your executive summary:

1. What entropy becomes is depends on how you assign probabilities to the outcome space.
2. Without a doubt, if you leave humans to choose PINs, they will choose certain values with much higher probability than others.
3. This means you can't assume the underlying distribution is uniform and say "entropy==number of outcomes".
4. If you take out the highest probability poor-choice options, entropy goes up.
5. Entropy, like probability of guessing correctly, says absolutely nothing about whether an attacker will get lucky and guess your PIN correctly. It simply says that in theory better entropy gives your attacker a harder time.

Now, to round out my answer, let us look at practicalities. If we are going to compare to passwords, or hash function output choices, or random data, PINs suck. If you give an attacker and defender free choice of PIN guess and no other information, the number of guesses to be right 50% of the time (birthday paradox) is ridiculously low. PINs would make lousy hash functions.

However, humans cannot memorise 128-bits of data very well, especially when drunk and trying to pay for a kebab using chip-and-pin. PINs are therefore a pragmatic compromise and with three guesses as a limit, aside from an attacker getting very lucky, you should be safe.

TL;DR Removing the choice of more likely PINs from your possible choices improves your chances when faced with an attacker that will not be guessing at random (i.e. most attackers).

---

Edit: I think this dicussion warrants some mathematics now. Here is what I am going to assume in my calculations:

1. We are using 4-digit PINs

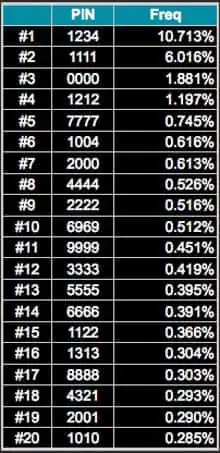
2. The data from Raesene's link is correct, i.e. that:

    #1     1234    10.713%
    #2     1111    6.016%
    #3     0000    1.881%
    #4     1212    1.197%
    #5     7777    0.745%
    #6     1004    0.616%
    #7     2000    0.613%
    #8     4444    0.526%
    #9     2222    0.516%
    #10    6969    0.512%
    #11    9999    0.451%
    #12    3333    0.419%
    #13    5555    0.395%
    #14    6666    0.391%
    #15    1122    0.366%
    #16    1313    0.304%
    #17    8888    0.303%
    #18    4321    0.293%
    #19    2001    0.290%
    #20    1010    0.285%
   

3. I am also going to assume that any PIN not mentioned in this list has an equal chance of being chosen from the remaining, "unallocated" probability (1-total probability consumed above). This is almost definitely incorrect, but we only have so much data.

To compute this, I used the following sage code:

def shannon_entropy(probabilities):
    contributions = [p * (-1*log(p,2)) for p in probabilities]
    return sum(contributions)

Computes the actual shannon entropy for a given set of probabilities.

import itertools
total_outcomes = 10.0^4
probability_random_outcome = 1 / total_outcomes
probability_random_outcome
maximum_entropy = -log(probability_random_outcome, 2)
maximum_entropy

maximum_entropy_probability_list = list(itertools.repeat(probability_random_outcome, total_outcomes))
maximum_entropy_calculated = shannon_entropy(maximum_entropy_probability_list)
print(maximum_entropy)
print(maximum_entropy_calculated)

Demonstrates my function accurately computes maximum entropy, by taking a list of 10^4 probabilities, each at 1/10^4.

Then

probability_list_one = [10.713/100, 6.016/100, 1.881/100, 1.197/100, 0.745/100, 0.616/100, 0.613/100, 0.526/100,0.516/100, 0.512/100, 0.451/100, 0.419/100, 0.395/100, 0.391/100, 0.366/100, 0.304/100, 0.303/100,0.293/100,0.290/100,0.285/100]

outcome_count_one = 10^4 - len(probability_list_one)
print("Outcome count 1:", outcome_count_one)
probability_consumed_one = sum(probability_list_one)
print("Probability consumed by list: ", probability_consumed_one)
probability_ro_one = (1-probability_consumed_one)/outcome_count_one
entropy_probability_list_one = probability_list_one + list(itertools.repeat(probability_ro_one, outcome_count_one))
entropy_one = shannon_entropy(entropy_probability_list_one)
entropy_one

Here, as I said above, I take those 20 probabilities and assume the rest of the probabilities are distributed evenly between the remaining outcomes, by extending the list with each probability set evenly. The computation is performed.

probability_list_two = [6.016/100, 1.881/100, 1.197/100, 0.745/100, 0.616/100, 0.613/100, 0.526/100,0.516/100, 0.512/100, 0.451/100, 0.419/100, 0.395/100, 0.391/100, 0.366/100, 0.304/100, 0.303/100,0.293/100,0.290/100,0.285/100]

outcome_count_two = 10^4 - len(probability_list_two)-1
print("Outcome count 2:", outcome_count_two)
probability_consumed_two = sum(probability_list_two)
print("Probability consumed by list: ", probability_consumed_two)
probability_ro_two = (1-probability_consumed_two)/outcome_count_two
entropy_probability_list_two = probability_list_two + (list(itertools.repeat(probability_ro_two, outcome_count_two)))
entropy_two = shannon_entropy(entropy_probability_list_two)
entropy_two

In this instance, I remove the most likely PIN, 1111 and recompute entropy.

From these results, you can see that randomly chosing a PIN has 13.2877 bits of entropy. Repeating this experiment with one PIN removed gives us 13.2876 bits

Choosing a PIN given those probabilities of choice for those 20 PINs and otherwise choosing randomly means your choice as 11.40 bits of entropy, out of a possible 13.2877 bits. From this base, blocking PIN 1111 and otherwise allowing the remaining 19 obvious PINs and all other PINs chosen with equal probability has entropy 12.33 bits, out of a possible 13.2876 bits.

I hope this explains why many of the answers are saying entropy is going down, rather than up. They're considering maximum possible entropy, rather than the average entropy (shannon entropy) of the system taking into account the possibility of choice. A better measure is the shannon entropy, since it takes into account the probability of each choice being made overall and so how an attacker will likely proceed in attacking.

As you can see, blocking that PIN 1111 significantly increases shannon entropy, at a slight cost to overall possible entropy. If you want to argue about entropy, basically, removing the PIN 1111 massively helps.

For reference that XKCD comic calculates entropy of poor passwords at about 28 bits and entropy of good ones higher, at 44 bits. Again it depends on what assumptions are being made as to the probabilities of certain choices but this should also show that PINs suck in terms of entropy and the N-tries limit for small N is the only sane way to proceed.

Public sage worksheet

Answer 3

This really depends on how the PIN is created:

• If the PIN is generated, make sure the distribution is uniform and don't exclude any combinations. That will maximize the entropy.

• If the PIN is chosen by a human operator, it makes perfect sense to exclude some combinations. I wouldn't go as far as rejecting half of the combinations, but if you do, you should also consider reject PINs starting with 0 1 and 2 (think birth years and dates) then PINs corresponding to physical key layouts like 2580 and 1379 and so on and so forth. Just make sure you stop before you end up allowing a single 8068 PIN which this study has found to be the least probable.

What you should do for human-chosen PINs is excluding the most common combinations: 1234 and 1111 alone account for almost 17% of all PINs in use, and 20 most popular PINs account for almost 27%. Those include each digit repeated 4 times and popular combinations like 1212 and 4321.

Edit: on a second thought, I think you should exclude most common combinations in any case. Even if your PIN is randomly generated, the attacker may not know that, in which case they will most probably try those combinations first.

Answer 4

Entropy is a property of the password generation method, not the password.

If you decide to eliminate repeated digits - this decision lowers the entropy compared to generating a random sequence.

In fact, anything you come up with will have lower entropy than generating a random sequence.

---

And if you believe a randomly-generated password 1111 has a low entropy and is thus easier to brute-force, just go to any gambling place and bet on 1 four times in a row - it should be a sure win.

Answer 5

Restricting your available pool of numbers reduces the number of possible solutions, making it less secure.

Repeating digits is a common human weakness when choosing pin codes, which means it will be tried first by attackers. Thus, ruling out repeated numbers increases security.

As is often the case, the decision has both upsides and downsides depending on the specific attack you're defending against. You probably shouldn't over-think it, and consider wider-perspective changes (like not using a 4-digit pin, or adding a second factor, or having lockouts on incorrect tries) if you want to increase the security of the system.

Answer 6

It looks to me that most of the other answers are focussing on the wrong type of attack.

Since we are dealing with a very specific scenario (manual PIN input) we can optimize the PIN generation for the possible attack scenarios.

Dictionary Attack

From what I can gather from the question, we are talking about manual PIN input, so the attacker has to type out each PIN they try. So a brute force attack might take quite a while (say, you need two seconds for each PIN you try, it will take almost three hours on average). This is possible, but not the smartest approach.

So when a brute force attack is unfeasible, you can instead try a dictionary attack. Here you try the most common PINs first. If this fails you can always resort to a brute force attack later. With dictionary attacks, entropy does not matter that much anymore. Here it matters whether the password is in the dictionary or not. Since the attacker most likely does not have a real dictionary of common PINs, they will have to come up with their dictionary on the fly. This would mean, the dictionary will probably be rather short and pattern-orientated. Possible PINs in the dictionary would be:

• Consecutive PINs (e.g. 0123 or 1234)
• PINs with four times the same digit (e.g. 2222)
• maybe also PINs with only three times the same digit

By eliminating these few passwords you don't lower your keyspace size by much but you can easily defend against dictionary attacks. Similar strategies are used by websites that don't allow you to use common or easy to guess passwords (e.g. using the username as the password)

Brute Force Attack

Next we can try to optimize against possible brute force attacks. This might help a lot less for a higher cost, so this might not be worthwhile. There are two main strategies how an human attacker can perform brute force attacks: either just enter random PINs or start with 0000 and count up (or 9999 and count down). So PINs like 0001 or 9998 might be a bad choice since someone performing a brute force attack might find them rather quickly. So maybe exclude PINs starting with 0 or 9.


Following these rules you should not loose too many possible passwords, but you might be able to strengthen your PIN against the most common attack strategies for this specific scenario.

Answer 7

Don't have enough to comment but have a recommendation. PIN that are typed using a single button (or a simple pattern of buttons) are easier observed by a shoulder surfer. In elementary school the teacher thought they did me a favor by making my password 4321 and some jerk watched my finger move in a straight line and told everyone my password.

I advise making a list of weak PINs that are susceptible to this, and then subtracting them from fully randomly generated PINs.

Answer 8

It depends on the implementation. Eliminating consecutive numbers will reduce the keyspace by .1% but has some benefits to physical security that may make it worth the tradeoff.

A lot of good clever answers here, main point being that instead of making it more secure, you're making the keyspace smaller (however negibly, 10 out of 10.000).

The top answers however fail to touch on the physical aspect of entering a pin. Visual and thermovisual extraction are a real danger these days. In other words, bad guys shoulder-surfing your pincode either with their eyes, a telescope, a skimming camera on the ATM or even thermal imaging cameras.

That last one is more recent, and especially nasty as a skimmer can walk up to a pin pad and look at the heat signature, even if you covered the pad well.

Having a consecutive pin will hurt security in this area; it reduces the complexity of the physical location of the numbers by a horrible amount. Even if you covered your hand, chances are the attacker will guess the button you pressed four times before a lockout happens. On a phone, if there is a big grease spot on the zero, that's the one i'll try first.

Answer 9

On my phone, the PIN deliberately uses one of the numbers twice in a row, in order to make it harder to guess because:

• The amount of "grease spots" does not match the number of digits
• A "shoulder surfer" will have a (little) harder time to distinguish double tapping from single tapping

Addendum: The phone in question allows for a custom lenght of the PIN, thus an attacker (not observing pin entry) does not know the number of digits in use.

Answer 10

You should make a specific list of “weak keys” in advance, that are what someone would try guessing. This includes important dates, addresses, etc. and may include 1111 if people actually would try that when guessing.

Then make a random draw, and filter against the (short) list. If the list is not short but systematic, (e.g. no repeated digits, no legal dates) then you wind up with too few possibilities which starts making it easier to guess again.

Answer 11

In 2012, a researcher compiled a list of the most popular PIN codes from a number of data breaches. What he found was that the most popular PINs were either:

1. Sequences, such as 1234 or 7777
2. Dates, like 2001
3. Pop culture references, such as 0007 (from James Bond's code number 007)
4. Easy to type, such as 2580 (numbers which lie in a straight line on many keypads)

Here is the top 20 (which does not include all examples given above):

So, sequences are bad. So are PINs that are easily memorable without a mnemonic. However, pins which have the same digit more than once are not necessarily bad, too.

Case in point:

At the other end of the scale, the least frequently used number I found in my dataset was 8068. Out of all the combinations of numbers this appeared to be the least interesting. It's not a date in history, it's not a pattern, it's not a birthday, it's not easy to type. It's the perfect pin … or it would have been until now.

So now you know.

Answer 12

There may be some attacks that vary in effectiveness, depending on the number of repeated digits.

For example, lets say someone applies a light dust to the keypad of your teller machine. You put your card in, cover your hands as you type in your pin, check your balance, then wonder off. As you go, someone picks your pocket, gets your card.

They now have your card, and can see which buttons have their dusting disturbed - they know the digits, but not the order.

If they see you pressed the digits 2, 3, 6, and 8, then your pin could be one of the following:

2368, 2386,   2638, 2683,   2836, 2863, 
3268, 3286,   3628, 3682,   3826, 3862,
6238, 6283,   6328, 6382,   6823, 6832,
8236, 8263,   8326, 8362,   8623, 8632

24 possibilities. With 3 guesses, they have a 1/8 chance of guessing right.

Here are the possibilities with 4 digits, one of which is repeated: 2, 3 and 6:

2236, 2263, 2326, 2336, 2362, 2363, 
2366, 2623, 2632, 2633, 2636, 2663, 
3226, 3236, 3262, 3263, 3266, 3326, 
3362, 3622, 3623, 3626, 3632, 3662, 
6223, 6232, 6233, 6236, 6263, 6322, 
6323, 6326, 6332, 6362, 6623, 6632

There are 36 of these. Odds of guessing this in 3 attempts is 1/12. Better odds!

Lets try this again, this time with only two digits:

2223, 2232, 2233, 2322, 2323, 2332, 2333, 
3222, 3223, 3232, 3233, 3322, 3323, 3332

14 combinations, over 1/5 chance of guessing with 3 tries.

Obviously, with only one digit, there is only one solution, and it can be guessed straight away.

Of course, if the digits in your pin are 1, 6 and 9, I'm going to guess that you were born in 1961, 1966, 1969, or 1996 - if I see you walk off, I should be able to guess if you're 21 or 48ish, which means 3 guesses mis probably all I need.

Answer 13

You are right that rules to remove patterns would hurt your key space, but it doesn't lower anythings entropy as the entropy is from your hardware, your TRNG machine is allowed to output a repeating digit now and again.

On the math if you don't want to see a repeating digit like 9 in '0919' then your math is right, but if you mean repeating digit like 9 in '0991' then your are left with 7190 out of 10000.

But depending on what you are thinking with "four digits containing some property or pattern" you whittle it down further, remove any patterns like '12', 321' or '34', remove any non primes, then you only have a handful (~300 out of 10000) of uninteresting numbers.

Answer 14

Avoid using the same digit consecutive. The delay between the same digit will be shorter then the delay between different digits (since your finger is already on the button), giving important information away.

Answer 15

4 digit pins are easily cracked in seconds with the right equipment. Why use such a laughably short pin when exploits like Reaver have proven that 4 digits is not enough (assuming your pin can be brute forced)

And if it can't be brute forced, what are you worried about? The odd's of someone guessing it are still 1 in 10,000, regardless of whether the pin is 1743 or 1111. You're taking a risk always with a shorter pin, and it would be ill advised to not accept repeated sequences as you're drastically lowering the entropy.

If your mind is set on this though, you could just make sure your generator keeps producing values until it has a unique digit in each position. This method would seem most logical for what you're trying to accomplish, and won't reduce the entropy if you still allow 1111, for example, to be generated although not used (repeatedly generating numbers until it finds one with unique digit in each position, and throwing away ones which are not)