Difference between signing and decrypting
I think your confusion stems from the fact that signing is in theory indeed somewhat similar to decryption for some algorithms (for example RSA).
Wikipedia for example phrases it like this:
Suppose Alice wishes to send a signed message to Bob. She can use her
own private key to do so. She produces a hash value of the message,
raises it to the power of d (modulo n) (as she does when decrypting a
message), and attaches it as a "signature" to the message.
This is however not how it is done in practice, and it is why your approach doesn't work.
For a more in-depth explanation of signing and decryption see eg here:
In the abstract world of textbooks, RSA signing and RSA decryption do
turn out to be the same thing. In the real world of implementations,
they are not. So don't ever use a real-world implementation of RSA
decryption to compute RSA signatures. In the best case, your
implementation will break in a way that you notice. In the worst case,
you will introduce a vulnerability that an attacker could exploit.
Furthermore, don't make the mistake of generalizing from RSA to
conclude that any encryption scheme can be adapted as a digital
signature algorithm. That kind of adaptation works for RSA and El
Gamal, but not in general.
Regarding PGP, it doesn't sign the message itself, but instead it signs a hash digest of the message:
PGP uses a cryptographically strong hash function on the plaintext
the user is signing. This generates a fixed-length data item known as
a message digest. (Again, any change to the information results in a
totally different digest.)
Then PGP uses the digest and the private key to create the
"signature." PGP transmits the signature and the plaintext together.
Upon receipt of the message, the recipient uses PGP to recompute the
digest, thus verifying the signature. PGP can encrypt the plaintext or
not; signing plaintext is useful if some of the recipients are not
interested in or capable of verifying the signature.
Here is an image describing the process:
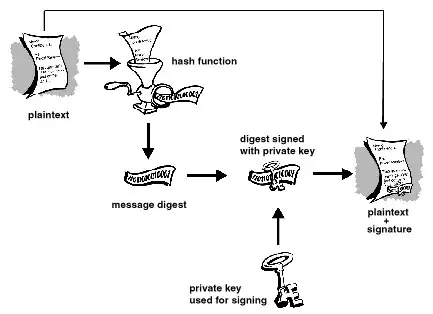
Why you can't just decrypt a message to sign it
The above is all well and good, and we know that we shouldn't decrypt messages to sign them in practice, but why can't we do it just for fun?
Because that's not how PGP or GPG work. A full explanation of the inner workings would probably be too much for this question, but see for example How does GPG verify succesful decryption?.
In short, PGP doesn't just do some mod operation on the data on decryption, the .pgp format is well defined and contains various information. Note also that PGP doesn't actually use asymmetric encryption such as RSA on the message itself, but on a key which is then used to symmetrically encrypt the message.
Conclusion
To summarize, if you were to use plain RSA, you could use decryption to sign a message (but you shouldn't), but PGP and GPG aren't plain RSA, so you can't just decrypt a message to sign it.
