I think it's easier to split this into its component parts, and consider them as separate entities: AES and CBC.
AES itself does not "basically consist of XORing together chunks of the block" - it's a much more complicated affair. Ignoring the internals of it for a moment, AES is considered secure in that without knowing the key, it's practically impossible to recover the plaintext or any information about the plaintext given only an encrypted block, or even in situations where you're given parts of the plaintext and you need to find the remainder. Without the key, AES might as well be a one-way function (and there are MAC schemes which rely upon this!). Discussing the technicalities around the security of AES and similar block ciphers is extremely involved and not something I can cover in an answer, but suffice to say that thousands of cryptographers have been looking at it for almost two decades and nobody has found anything remotely practical in terms of an attack.
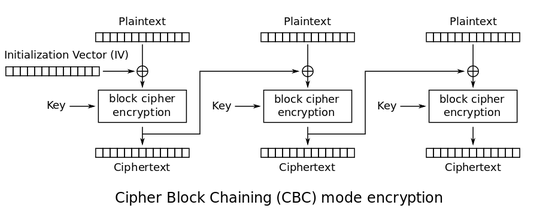
The diagram you posted above describes CBC. Block ciphers, such as AES, aim to be secure for encrypting one block with a secret key. The problem is that we rarely want to just encrypt one block, but rather a data stream of indeterminate length. This is where block modes, like CBC, come into play.
Block modes aim to make ciphers secure for encrypting multiple blocks with the same key. The most simple block mode is ECB, which offers zero security in this regard. ECB involves independently encrypting each block with the same key, without any data fed between blocks. This leaks information in two ways: first, if you have two identical plaintext blocks, you'll get two identical ciphertext blocks if you use the same key; second, you'll get two identical ciphertext streams for two encryptions of the same message with the same key. This is a problem as it leaks information about the plaintext.
CBC solves this problem by introducing a "cascading" effect. Each plaintext block is xor'ed with the previous ciphertext block, resulting in originally equal plaintext blocks no longer being equal at the encryption step, thus no longer producing equal ciphertext blocks. For the first plaintext block, there is no previous ciphertext block (you haven't encrypted anything yet), and this is where the IV comes in. Consider, for a moment, what would happen if instead of an IV we just used zeroes for the -1th block (i..e the imaginary ciphertext block "before" the first plaintext block). While the cascade effect would make equal plaintext blocks produce different ciphertext blocks, the same entire message would cascade the same way each time, resulting in an identical ciphertext when the same full message is encrypted multiple times with the same key. The IV solves this. By picking a unique IV, no two ciphertexts are ever the same, regardless of whether the plaintext message being encrypted is the same or different each time.
This should, hopefully, help you understand why the IV doesn't need to be secret. Knowing the IV doesn't get an attacker anywhere, because the IV is only there to ensure non-equality of ciphertexts. The secret key is what protects the actual data.
To emphasise this even further, you don't even need the IV to decrypt all but the very first block. The decryption process for CBC works in reverse: decrypt a block using the secret key, then xor the result with the previous ciphertext block. For all but the very first block, you know the previous ciphertext block (you've got the ciphertext) so decryption is just a case of knowing the key. The only case where you need the IV for decryption is the very first encrypted block, where the previous ciphertext block is imaginary and replaced with the IV.