Task 1: Key Concepts about Using the T-Test Statistic

The t-test is used to test the null hypothesis that two population means or proportions, θ₁ and θ_2, are equal or, equivalently, that the difference between two population means or proportions is zero. To test this hypothesis, assuming the covariance is small, as is the case with NHANES data, the following formula is used:      

Equation for t-Test  Where Covariance is Small

 

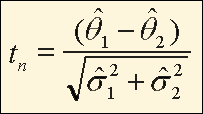
where,

₁ is an estimate of the first population mean or proportion based on a probability sample,

₁ is an estimate of the standard error of  ₁,

₂ is an estimate of the second population mean or proportion,

and ₂ is an estimate of the standard error of  ₂.

In instances where only a small number (<30) of independent pieces of information are available with which to estimate the quantity [₁ - ₂], the t-statistic given above follows a Student's t distribution with zero mean and unit variance, and with a number of degrees of freedom corresponding to the number of independent pieces of information.  In a simple random sample, the number of independent pieces of information is generally equal to the number of people in the sample minus one.  In NHANES, however, the number of independent pieces of information is substantially lower due to the multi-stage probability sample design.  In NHANES, this number (referred to as degrees of freedom) is equal to the number of PSUs minus the number of strata (see “Module 12: Sample Design” of the Continuous NHANES Tutorial for more information).

The equality of means is usually tested at the 0.05 level of significance.  However, at the 0.05 level of significance, some differences that are not meaningful (usually very small) are significant because of the large sample size.