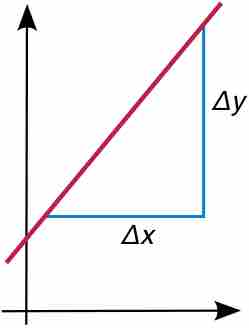
Slope
The slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline. Slope is normally described by the ratio of the "rise" divided by the "run" between two points on a line. The line may be practical (as for a roadway) or in a diagram.
Slope
The slope of a line in the plane is defined as the rise over the run,
The slope of a line in the plane containing the x and y axes is generally represented by the letter m, and is defined as the change in the y coordinate divided by the corresponding change in the x coordinate, between two distinct points on the line. This is described by the following equation:
The Greek letter delta,
Intercept
Using the common convention that the horizontal axis represents a variable
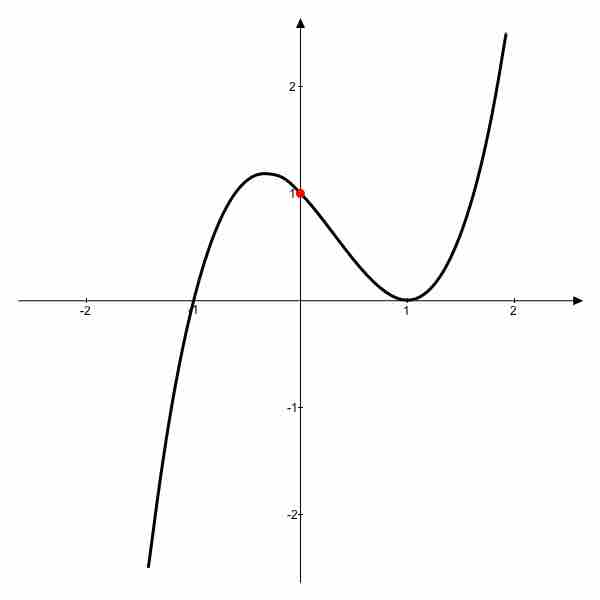
Intercept
Graph with a
If the curve in question is given as
Some 2-dimensional mathematical relationships such as circles, ellipses, and hyperbolas can have more than one
Analogously, an