The
Alternatively, we could carry out pairwise tests among the treatments (for instance, in the medical trial example with four treatments we could carry out six tests among pairs of treatments). The advantage of the ANOVA
The formula for the one-way ANOVA
or
The "explained variance," or "between-group variability" is:
where
The "unexplained variance", or "within-group variability" is:
where
Note that when there are only two groups for the one-way ANOVA
Example
Four sororities took a random sample of sisters regarding their grade means for the past term. The data were distributed as follows:
- Sorority 1: 2.17, 1.85, 2.83, 1.69, 3.33
- Sorority 2: 2.63,1.77, 3.25, 1.86, 2.21
- Sorority 3: 2.63, 3.78, 4.00, 2.55, 2.45
- Sorority 4: 3.79, 3.45, 3.08, 2.26, 3.18
Using a significance level of 1%, is there a difference in mean grades among the sororities?
Solution
Let
Distribution for the test:
where
Calculate the test statistic:
Graph:
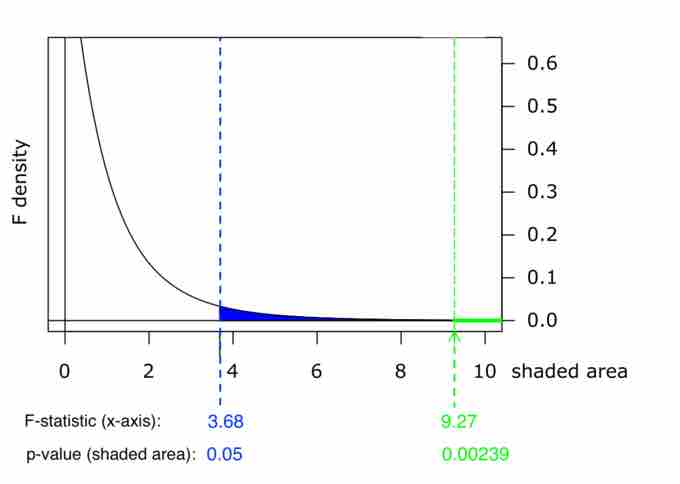
Graph of $p$ -Value
This chart shows example p-values for two F-statistics: p = 0.05 for F = 3.68, and p = 0.00239 for F = 9.27. These numbers are evidence of the skewness of the F-curve to the right; a much higher F-value corresponds to an only slightly smaller p-value.
Probability statement:
Compare
Make a decision: Since
Conclusion: There is not sufficient evidence to conclude that there is a difference among the mean grades for the sororities.