The odds of an outcome is the ratio of the expected number of times the event will occur to the expected number of times the event will not occur. Put simply, the odds are the ratio of the probability of an event occurring to the probability of no event.
An odds ratio is the ratio of two odds. Imagine each individual in a population either does or does not have a property
- Compute the odds that an individual in the population has
$A$ given that he or she has$B$ (probability of$A$ given$B$ divided by the probability of not-$A$ given$B$ ). - Compute the odds that an individual in the population has
$A$ given that he or she does not have$B$ . - Divide the first odds by the second odds to obtain the odds ratio.
If the odds ratio is greater than one, then having
In more technical language, the odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic and plays an important role in logistic regression.
Example
Suppose that in a sample of
This example also shows how odds ratios are sometimes sensitive in stating relative positions. In this sample men are
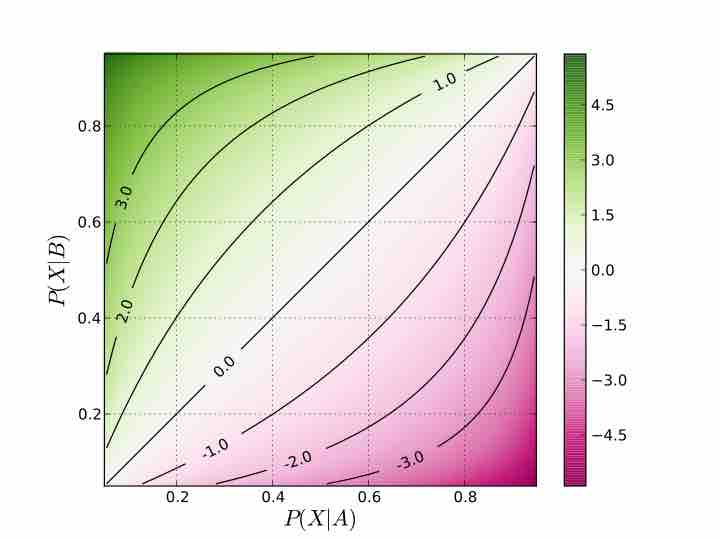
Odds Ratios
A graph showing how the log odds ratio relates to the underlying probabilities of the outcome