The tool of normal approximation allows us to approximate the probabilities of random variables for which we don't know all of the values, or for a very large range of potential values that would be very difficult and time consuming to calculate. We do this by converting the range of values into standardized units and finding the area under the normal curve. A problem arises when there are a limited number of samples, or draws in the case of data "drawn from a box." A probability histogram of such a set may not resemble the normal curve, and therefore the normal curve will not accurately represent the expected values of the random variables. In other words, the scope of the normal approximation is dependent upon our sample size, becoming more accurate as the sample size grows. This characteristic follows with the statistical themes of the law of large numbers and central limit theorem (reviewed below).
Law of Large Numbers
The law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.
The law of large numbers is important because it "guarantees" stable long-term results for the averages of random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. It is important to remember that the LLN only applies (as the name indicates) when a large number of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a streak of one value will immediately be "balanced" by the others.
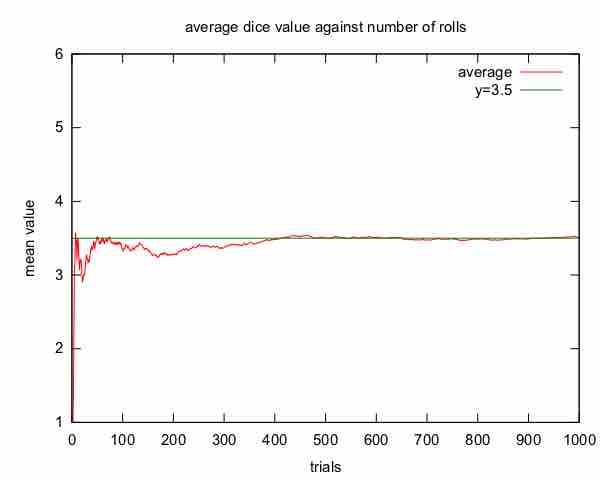
Law of Large Numbers
An illustration of the law of large numbers using a particular run of rolls of a single die. As the number of rolls in this run increases, the average of the values of all the results approaches 3.5. While different runs would show a different shape over a small number of throws (at the left), over a large number of rolls (to the right) they would be extremely similar.
Central Limit Theorem
The central limit theorem (CLT) states that, given certain conditions, the mean of a sufficiently large number of independent random variables, each with a well-defined mean and well-defined variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common form, the random variables must be identically distributed. In variants, convergence of the mean to the normal distribution also occurs for non-identical distributions, given that they comply with certain conditions.
More precisely, the central limit theorem states that as
Approximates the normal distribution with mean 0 and variance
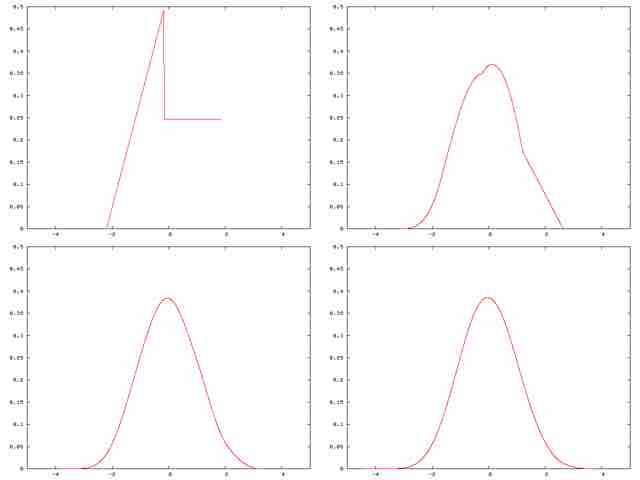
Central Limit Theorem
A distribution being "smoothed out" by summation, showing original density of distribution and three subsequent summations