An object with constant velocity has zero acceleration. A motionless object still has constant (zero) velocity, so motionless objects also have zero acceleration. Newton's second law states that:
so objects with constant velocity also have zero net external force. This means that all the forces acting on the object are balanced -- that is to say, they are in equilibrium.
This rule also applies to motion in a specific direction. Consider an object moving along the x-axis. If no net force is applied to the object along the x-axis, it will continue to move along the x-axis at a constant velocity, with no acceleration .
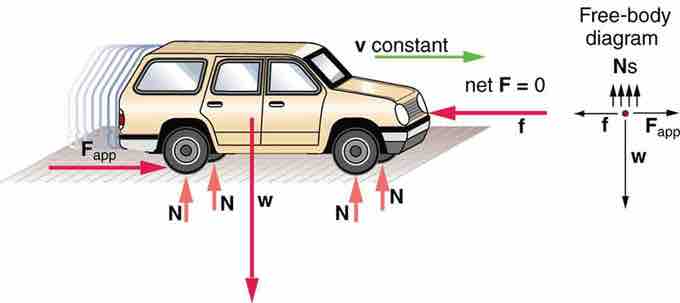
Car Moving at Constant Velocity
A moving car for which the net x and y force components are zero
We can easily extend this rule to the y-axis. In any system, unless the applied forces cancel each other out (i.e., the resultant force is zero), there will be acceleration in the direction of the resultant force. In static systems, in which motion does not occur, the sum of the forces in all directions always equals zero. This concept can be represented mathematically with the following equations:
This rule also applies to rotational motion. If the resultant moment about a particular axis is zero, the object will have no rotational acceleration about the axis. If the object is not spinning, it will not start to spin. If the object is spinning, it will continue to spin at the same constant angular velocity. Again, we can extend this to moments about the y-axis as well. We can represent this rule mathematically with the following equations: