When a current travels in a loop that is exposed to a magnetic field, that field exerts torque on the loop. This principle is commonly used in motors, in which the loop is connected to a shaft that rotates as a result of the torque. Thus, the electrical energy from the current is converted to mechanical energy as the loop and shaft rotate, and this mechanical energy is then used to power another device .
Torque on a Current Loop
Electrical energy from the current is converted to mechanical energy as the loop and shaft rotate, and this mechanical energy is then used to power another device.
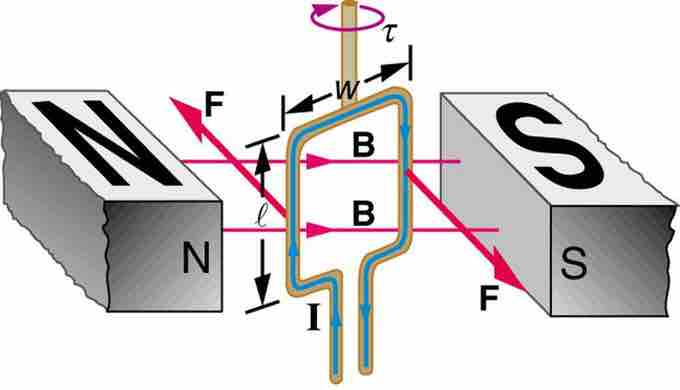
In this model, the north and south poles of magnets are denoted by N and S, respectively. In the center is a rectangular wire loop of length l and width w, carrying current I. The effect of magnetic field B on the current-carrying wire exerts torque τ.
To understand the torque, we must analyze the forces acting on each segment of the loop. Assuming a constant magnetic field, we can conclude that the forces on the top and bottom parts of the loop are equal in magnitude and opposite in direction, and thus produce no net force. Incidentally, those forces are vertical and thus parallel to the shaft.
However, as illustrated by (a) in the figure below, the equal but opposite forces produce a torque that acts clockwise .
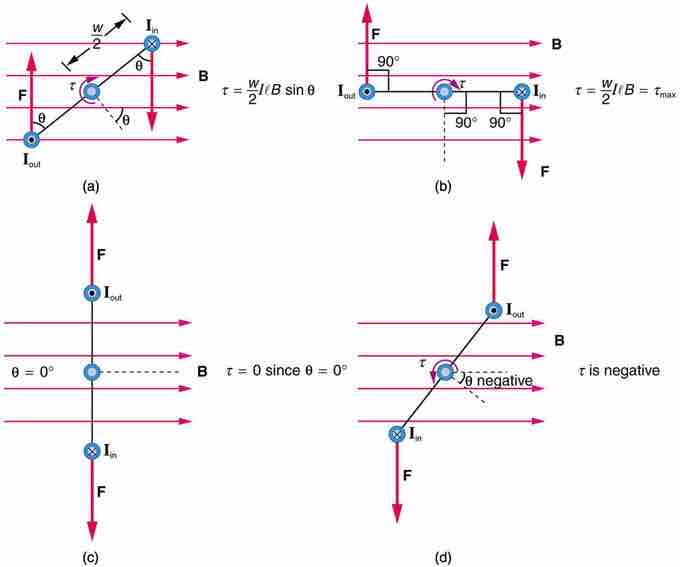
Varying torque on a charged loop in a magnetic field
Maximum torque occurs in (b), when is 90 degrees. Minimum torque is 0, and occurs in (c) when θ is 0 degrees. When loop rotates past =0, the torque reverses (d).
Given that torque is calculated from the equation:
where F is force on the rotating object, r is the distance from the pivot point that the force is applied, and θ is the angle between r and F, we can use the sum of two torques (the forces act on either side of the loop) to find the total torque:
Note that r is equal to w/2, as illustrated.
To find torque we still must solve for F from the magnetic field B on the current I. The rectangle has length l, so F=IlB. Replacing F with IlB in the torque equation gives:
Note that the product of w and l is included in this equation; those terms can be replaced with area (A) of the rectangle. If another shape of wire is used, its area can be inserted in the equation regardless of shape (whether circular, square, or otherwise).
Also note that this equation of torque is for a single turn. Torque increases proportionally according to number of turns (N). Thus, the general equation for torque on a loop of any shape, of N turns, each of A area, carrying I current and exposed to a magnetic field B is a value that fluctuates as the loop rotates, and can be calculated by: