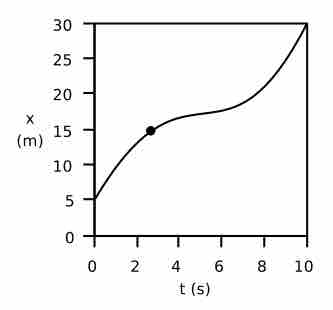
Typically, motion is not with constant velocity nor speed. While driving in a car, for example, we continuously speed up and slow down. A graphical representation of our motion in terms of distance vs. time, therefore, would be more variable or "curvy" rather than a straight line, indicating motion with a constant velocity as shown below. (We limit our discussion to one dimensional motion. It should be straightforward to generalize to three dimensional cases.)
Motion with Changing Velocity
Motion is often observed with changing velocity. This would result in a curvy line when graphed with distance over time.
To calculate the speed of an object from a graph representing constant velocity, all that is needed is to find the slope of the line; this would indicate the change in distance over the change in time. However, changing velocity it is not as straightforward.
Since our velocity is constantly changing, we can estimate velocity in different ways. One way is to look at our instantaneous velocity , represented by one point on our curvy line of motion graphed with distance vs. time. In order to determine our velocity at any given moment, we must determine the slope at that point. To do this, we find a line that represents our velocity in that moment, shown graphically in. That line would be the line tangent to the curve at that point. If we extend this line, we can easily calculate the displacement of distance over time and determine our velocity at that given point. The velocity of an object at any given moment is the slope of the tangent line through the relevant point on its x vs. t graph.
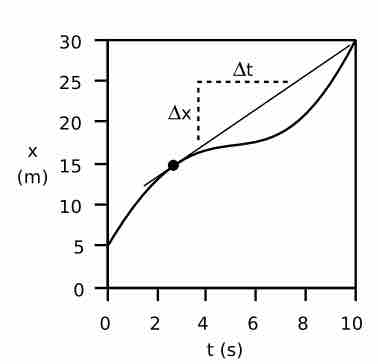
Determining instantaneous velocity
The velocity at any given moment is defined as the slope of the tangent line through the relevant point on the graph
In calculus, finding the slope of curve f(x) at x=x0 is equivalent to finding the first derivative:
One interpretation of this definition is that the velocity shows how many meters the object would travel in one second if it continues moving at the same speed for at least one second.