COMPOUND LENSES
In contrast to a simple lens, which consists of only one optical element, a compound lens is an array of simple lenses (elements) with a common axis. The use of multiple elements allows for the correction of more optical aberrations, such as the chromatic aberration caused by the wavelength-dependent index of refraction in glass, than is possible using a single lens. In many cases these aberrations can be compensated for to a great extent by using a combination of simple lenses with complementary aberrations.
The simplest case is where lenses are placed in contact: if the lenses of focal lengths f1 and f2 are "thin", the combined focal length f of the lenses is given by
Since 1/f is the power of a lens, it can be seen that the powers of thin lenses in contact are additive.
If two thin lenses are separated in air by some distance d (where d is smaller than the focal length of the first lens), the focal length for the combined system is given by
BACK FOCAL LENGTH
The distance from the second lens to the focal point of the combined lenses is called the back focal length (BFL).
As d tends to zero, the value of the BFL tends to the value of f given for thin lenses in contact.
If the separation distance is equal to the sum of the focal lengths (d = f1+f2), the combined focal length and BFL are infinite. This corresponds to a pair of lenses that transform a parallel (collimated) beam into another collimated beam (see ). This type of system is called an afocal system, since it produces no net convergence or divergence of the beam. Two lenses at this separation form the simplest type of optical telescope. Although the system does not alter the divergence of a collimated beam, it does alter the width of the beam. The magnification of such a telescope is given by
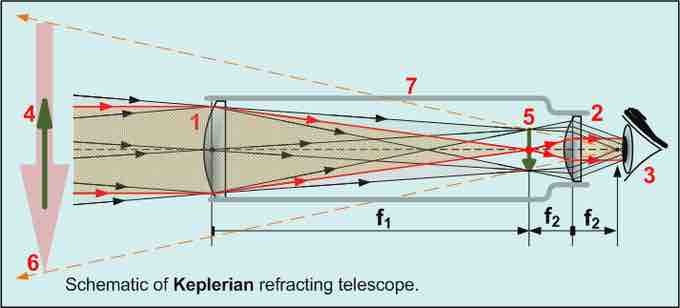
Keplerian Telescope
All refracting telescopes use the same principles. The combination of an objective lens 1 and some type of eyepiece 2 is used to gather more light than the human eye could collect on its own, focus it 5, and present the viewer with a brighter, clearer, and magnified virtual image 6. The magnification can be found by dividing the focal length of the objective lens by the focal length of the eyepiece.
which is the ratio of the input beam width to the output beam width. Note the sign convention: a telescope with two convex lenses (f1 > 0, f2 > 0) produces a negative magnification, indicating an inverted image. A convex plus a concave lens (f1 > 0 >f2) produces a positive magnification and the image is upright.
ACHROMATS
An achromatic lens or achromat is a lens that is designed to limit the effects of chromatic and spherical aberration. Achromatic lenses are corrected to bring two wavelengths (typically red and blue/violet) into focus in the same plane.
The most common type of achromat is the achromatic doublet, which is composed of two individual lenses made from glasses with different amounts of dispersion Typically, one element is a negative (concave) element made out of flint, which has relatively high dispersion, and the other is a positive (convex) element made of crown glass, which has lower dispersion. The lens elements are mounted next to each other, often cemented together, and shaped so that the chromatic aberration of one is counterbalanced by that of the other.
In the most common type (shown in ), the positive power of the crown lens element is not quite equaled by the negative power of the flint lens element. Together they form a weak positive lens that will bring two different wavelengths of light to a common focus. Negative doublets, in which the negative-power element predominates, are also made.
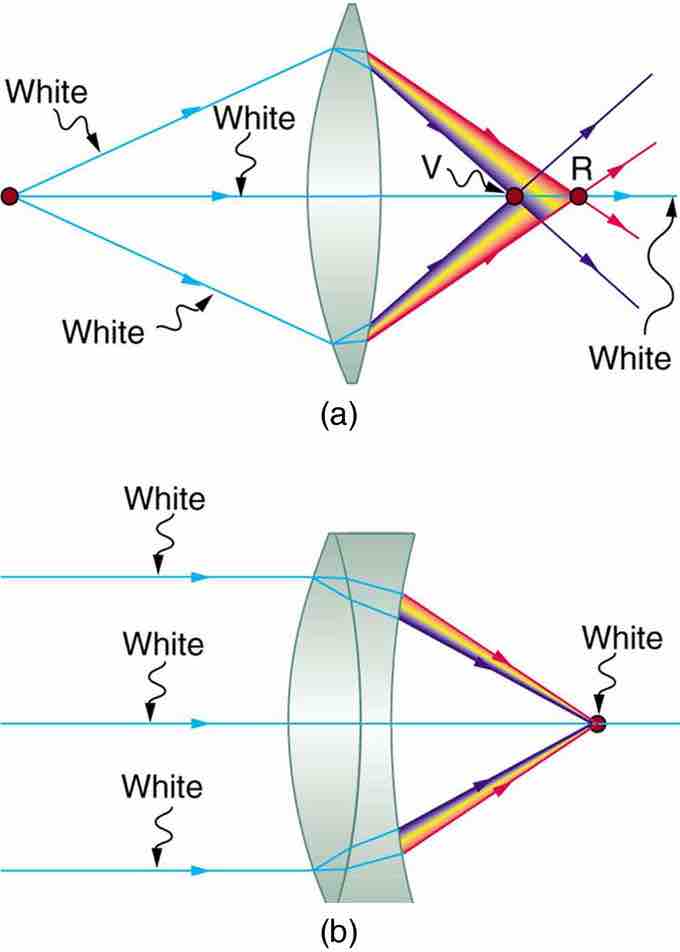
Achromatic Doublet
(a) Chromatic aberration is caused by the dependence of a lens's index of refraction on color (wavelength). The lens is more powerful for violet (V) than for red (R), producing images with different locations and magnifications. (b) Multiple-lens systems, such as this achromatic doublet, can partially correct chromatic aberrations, but they may require lenses of different materials and add to the expense of optical systems such as cameras.