Stand-Alone Risk
Recall that Beta is a number describing the correlated volatility of an asset or investment in relation to the volatility of the market as a whole. However, appraisers frequently value assets or investments, such as closely held corporations, as stand-alone assets. Total Beta is a measure used to determine the risk of a stand-alone asset, as opposed to one that is a part of a well-diversified portfolio. It is able to accomplish this because the correlation coefficient, R, has been removed from Beta. Total Beta can be found using the following formula:
Total Beta =
Another statistical measure that can be used to assess stand-alone risk is the coefficient of variation. In probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. In terms of finance, the coefficient of variation allows investors to determine how much volatility (risk) they are assuming in relation to the amount of expected return from an investment. Volatility is measured in the form of the investment's standard deviation from the mean return, thus the coefficient of variation is this standard deviation divided by expected return. A lower coefficient of variation indicates a higher expected return with less risk.
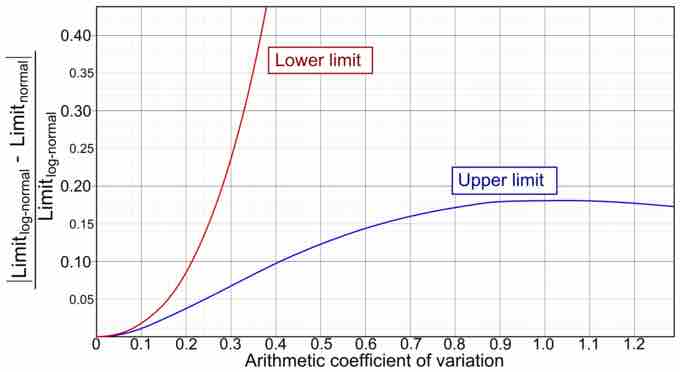
Coefficient of Variation
The coefficient of variation, an example of which is plotted in this graph, can be used to measure the ratio of volatility to expected return.
The coefficient of variation is a dimensionless number, meaning it is independent of the unit in which the measurement has been taken. For this reason, it becomes useful to us in finance to measure the risk of an investment in a way that it is not dependent upon other types of risk, such as that of the overall market.