Concept
Version 8
Created by Boundless
Absolute Convergence and Ratio and Root Tests
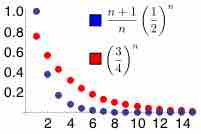
Ratio Test
In this example, the ratio of adjacent terms in the blue sequence converges to
Source
Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources: