Direction Fields
Direction fields, also known as slope fields, are graphical representations of the solution to a first order differential equation. They can be achieved without solving the differential equation analytically, and serve as a useful way to visualize the solutions.
The slope field is traditionally defined for differential equations of the following form:
It can be viewed as a creative way to plot a real-valued function of two real variables as a planar picture.
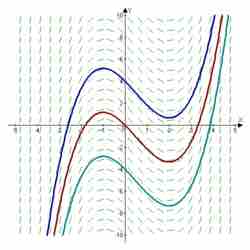
Example slope field
The slope field of
Specifically, for a given pair, a vector with the components is drawn at the point
Euler's Method
Consider the problem of calculating the shape of an unknown curve which starts at a given point and satisfies a given differential equation. Here, a differential equation can be thought of as a formula by which the slope of the tangent line to the curve can be computed at any point on the curve, once the position of that point has been calculated.The idea is that while the curve is initially unknown, its starting point, which we denote by
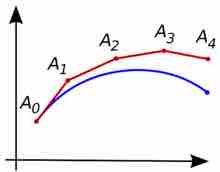
Euler's Method
Illustration of the Euler method. The unknown curve is in blue and its polygonal approximation is in red.
Take a small step along that tangent line up to a point,