Integration by substitution, also known as
Definite Integral
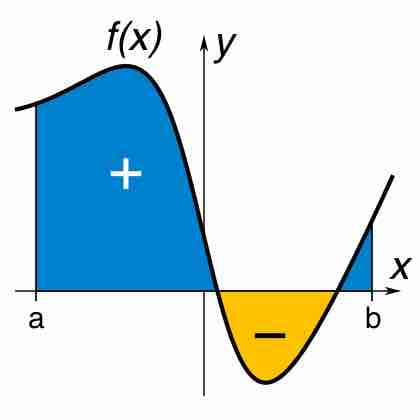
A definite integral of a function can be represented as the signed area of the region bounded by its graph.
Let
Using Leibniz notation, the substitution
and therefore, formally:
which is the required substitution for
The formula is used to transform one integral into another integral that is easier to compute. Thus, the formula can be used from left to right or from right to left in order to simplify a given integral. When used in the latter manner, it is often known as
For example, consider the following integral:
If we make the substitution
It is important to note that since the lower limit
Substitution can be used to determine antiderivatives if one chooses a relation between
Similar to our first example above, we can determine the following antiderivative with this method:
where