Vectors in the Plane

Vectors in the Plane

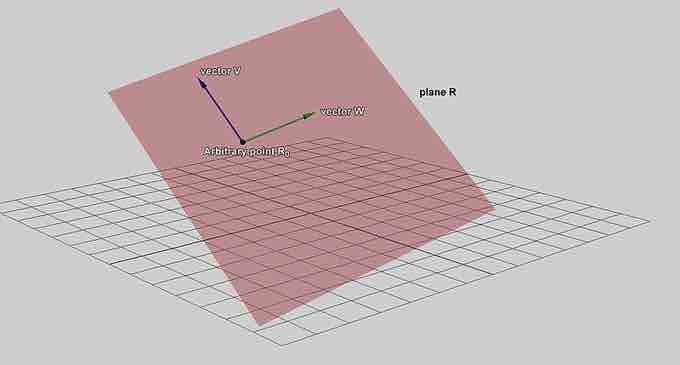
Planes in a three dimensional space can be described mathematically using a point in the plane and a vector to indicate its "inclination".

Normal Vector to a Plane

This plane may be described parametrically as the set of all points of the form$\mathbf R = \mathbf {R}_0 + s \mathbf{V} + t \mathbf{W}$, where $s$ and $t$ range over all real numbers, $\mathbf{V}$ and $\mathbf{W}$ are given linearly independent vectors defining the plane, and $\mathbf{R_0}$ is the vector representing the position of an arbitrary (but fixed) point on the plane. The vectors $\mathbf{V}$ and $\mathbf{W}$ can be visualized as vectors starting at $\mathbf{R_0}$ and pointing in different directions along the plane. Note that $\mathbf{V}$ and $\mathbf{W}$ can be perpendicular but not parallel.

General form of the equation of the plane

In order to find the equation of the plane, consider the following: Let $\mathbf{r}_0$ be the position vector of some point $\mathbf{P_0} = (x_0,y_0,z_0)$ , and let $\mathbf{n} = (a,b,c)$ be a nonzero vector.

The plane determined by this point and vector consists of those points $P$ , with position vector $\mathbf{r}$, such that the vector drawn from $P_0$ to $P$ is perpendicular to $\mathbf{n}$. Recall that two vectors are perpendicular if and only if their dot product is zero. As such, the equation that describes the plane is given by:

$\mathbf{n} \cdot (\mathbf{r}-\mathbf{r}_0)=0$

We can expand this equation in terms of its components to give:

$a (x-x_0)+ b(y-y_0)+ c(z-z_0)=0$

which we call the point-normal equation of the plane and is the general equation we use to describe the plane.