Concept
Version 12
Created by Boundless
Directional Derivatives and the Gradient Vector
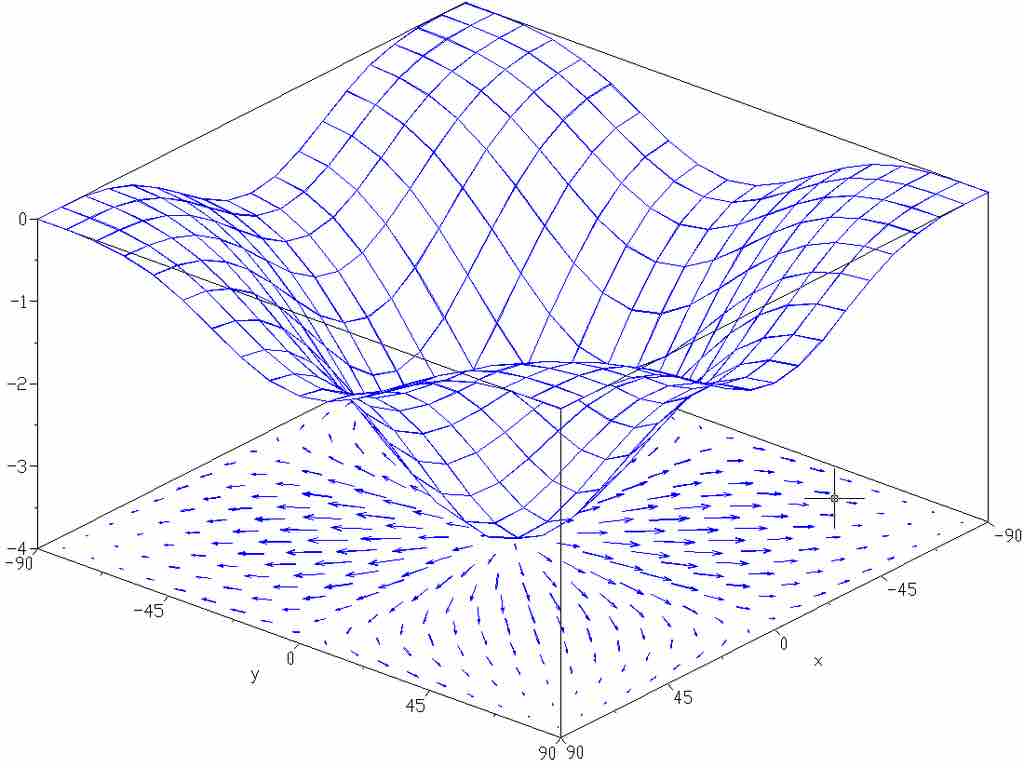
Gradient of a Function
The gradient of the function
Source
Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources: