Combined variation is used to describe the relationship between three or more variables that vary directly and inversely with one another. Before go deeper into the concept of combined variation, it is important to first understand what direct and inverse variation mean.
Direct and Inverse Variation
Simply put, two variables are in direct variation when the same thing that happens to one variable happens to the other. If x and y are in direct variation, and x is doubled, then y would also be doubled. The two variables may be considered directly proportional.
Two variables are said to be in inverse variation, or are inversely proportional, when an operation of change is performed on one variable and the opposite happens to the other. For example, if x and y are inversely proportional, if x is doubled, then y is halved.
Combined Variation
To have variables that are in combined variation, the equation must have variables that are in both direct and inverse variation, as shown in the example below.
Consider the equation:
where x, y, and z are variables and k is a constant known as the proportionality constant.
In this example, z varies directly as x and inversely as y.
Given values for any three of x, y, z, and k, the fourth can be found by substitution. For example, if z=12, x=4 and y=2, we can solve for k:
Practical Application
A practical example of combined variation is the Combined Gas Law, which relates the pressure (p), volume (v), moles (n), and temperature (T) of a sample of gas:
where R is a constant .
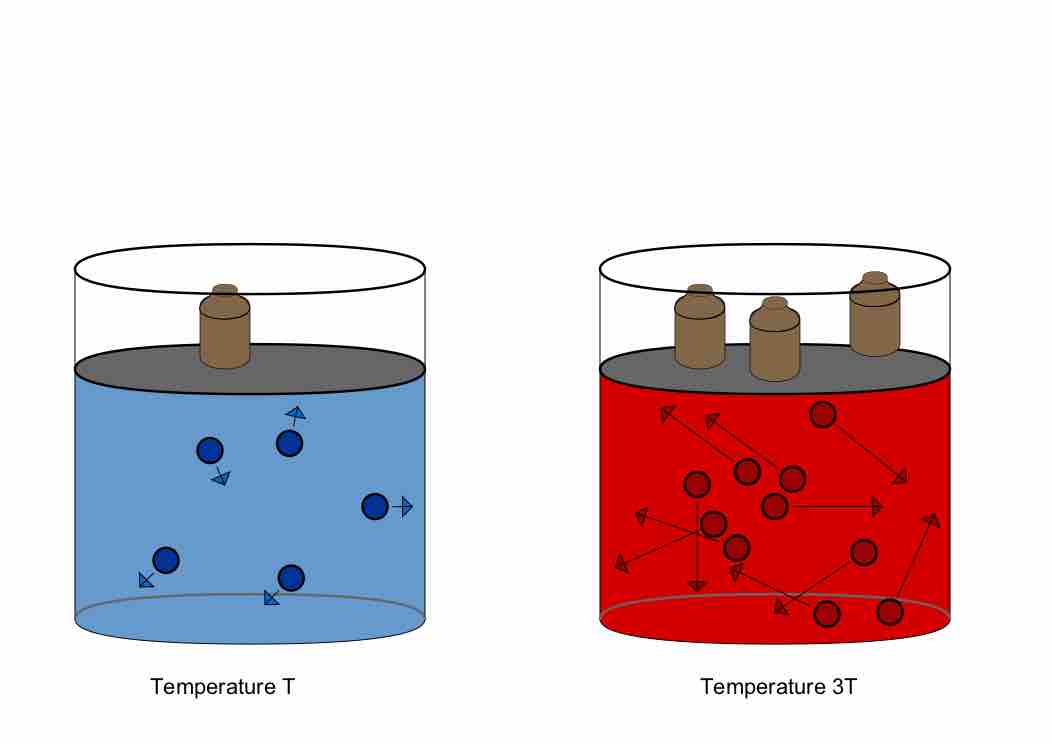
Illustration of Gay-Lussac's Law, derived from the Combined Gas Law
A constant amount of gas will exert pressure that varies directly with temperature. In this illustration, volume is held constant by an increased mass weighing down the lid of the container. If not for that extra mass, the lid would raise, increasing the volume and relieving the pressure.
Solving for P, we can determine the variation of the variables.
In the above equation, P varies directly with n and T, and inversely with V. Thus, pressure increases as temperature and moles increase. What's more, pressure decreases as volume increases.