A "real interval" is a set of real numbers such that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers
The interval of numbers between
Open and Closed Intervals
An open interval does not include its endpoints and is indicated with parentheses. For example,
A closed interval includes its endpoints and is denoted with square brackets rather than parentheses. For example,
To indicate that only one endpoint of an interval is included in that set, both symbols will be used. For example, the interval of numbers between 1 and 5, including 1 but excluding 5, is written as
The image below illustrates open and closed intervals on a number line.
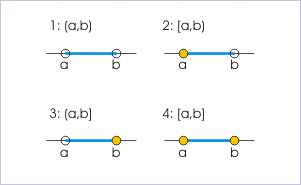
Intervals
Representations of open and closed intervals on the real number line.
Bounded and Unbounded Intervals
An interval is said to be bounded if both of its endpoints are real numbers.
Bounded intervals are also commonly known as finite intervals. Conversely, if neither endpoint is a real number, the interval is said to be unbounded.
For example,
the interval
The set of all real numbers is the only interval that is unbounded at both ends; the empty set (the set containing no elements) is bounded.
An interval that has only one real-number endpoint is said to be half-bounded, or more descriptively, left-bounded or right-bounded. For example, the interval