Now that we know what equations are, how do we go about visualizing them? For an equation with two variables,
Graphing an Equation in Two Variables
Let's start with the following equation:
We'll start by choosing a few
For the three values for
- If
$x=-2$ , then$y=-7$ . We plot the point$(-2,-7)$ . - If
$x=0$ , then$y=-3$ . We plot the point$(0,-3)$ . - If
$x=2$ , then$y=1$ . We plot the point$(2,1)$ .
Now we can connect the dots to visualize the graph of the equation:
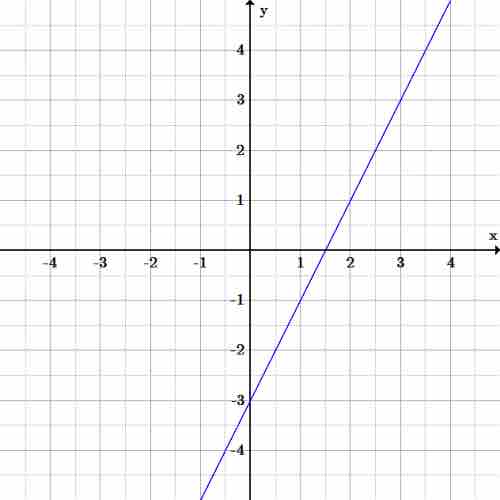
Graph of $y=2x-3$
The equation is the graph of a line through the three points found above. The line continues on to infinity in each direction, since there is an infinite series of ordered pairs of solutions.
Graphing Non-Linear Equations
Example 1
What graph will the following equation make?
Let's figure it out by choosing some points to plot.
First, let's try
So we plot
Note that we don't always have to choose values for
Through the same arithmetic as above, we get the ordered pairs
We still don't have enough points to really see what's going on, so let's choose some more. Let's try solving for
So that's two new points:
Now you can begin seeing that we're drawing a circle with a radius of 10:
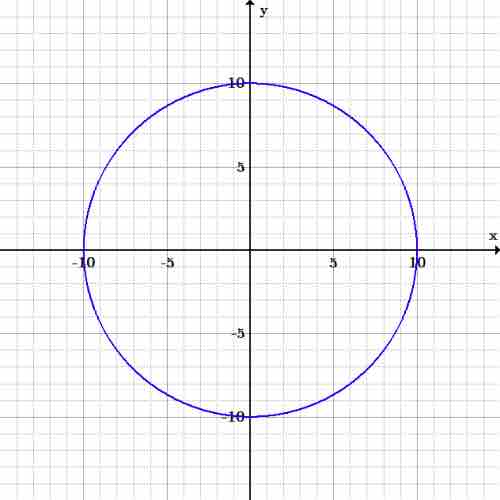
Graph of $x^2+y^2=100$
This is a graph of a circle with radius 10 and center at the origin.
Example 2
Let's try another example. This time let's use the following equation:
Again, let's plug in some numbers and begin plotting points.
Input values (for the independent variable
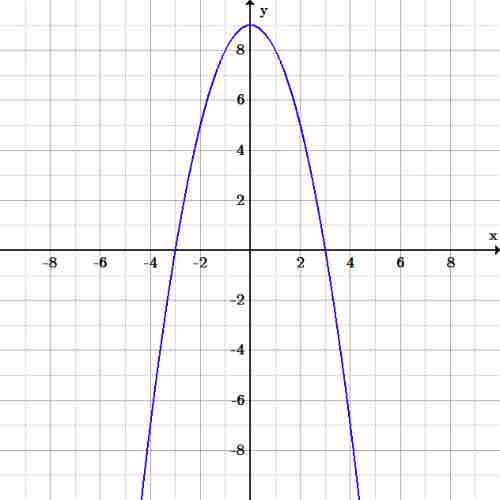
Graph of $y=-x^2+9$
This graph is of a parabola (a U-shaped open curve symmetric about a line). Parabolas can open up or down, right or left; they also have a maximum or minimum value.