Chance = Stochastic
In probability theory, a stochastic process--sometimes called a random process-- is a collection of random variables that is often used to represent the evolution of some random value, or system, over time. It is the probabilistic counterpart to a deterministic process (or deterministic system). Instead of describing a process which can only evolve in one way (as in the case, for example, of solutions of an ordinary differential equation), in a stochastic or random process there is some indeterminacy. Even if the initial condition (or starting point) is known, there are several (often infinitely many) directions in which the process may evolve.
In the simple case of discrete time, a stochastic process amounts to a sequence of random variables known as a time series--for example, a Markov chain. Another basic type of a stochastic process is a random field, whose domain is a region of space. In other words, a stochastic process is a random function whose arguments are drawn from a range of continuously changing values.
One approach to stochastic processes treats them as functions of one or several deterministic arguments (inputs, in most cases regarded as time) whose values (outputs) are random variables. Random variables are non-deterministic (single) quantities which have certain probability distributions. Random variables corresponding to various times (or points, in the case of random fields) may be completely different. Although the random values of a stochastic process at different times may be independent random variables, in most commonly considered situations they exhibit complicated statistical correlations.
Familiar examples of processes modeled as stochastic time series include stock market and exchange rate fluctuations; signals such as speech, audio, and video; medical data such as a patient's EKG, EEG, blood pressure, or temperature; and random movement such as Brownian motion or random walks.
Law of a Stochastic Process
The law of a stochastic process is the measure that the process induces on the collection of functions from the index set into the state space. The law encodes a lot of information about the process. In the case of a random walk, for example, the law is the probability distribution of the possible trajectories of the walk.
A random walk is a mathematical formalization of a path that consists of a succession of random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock, and the financial status of a gambler can all be modeled as random walks, although they may not be truly random in reality. Random walks explain the observed behaviors of processes in such fields as ecology, economics, psychology, computer science, physics, chemistry, biology and, of course, statistics. Thus, the random walk serves as a fundamental model for recorded stochastic activity.
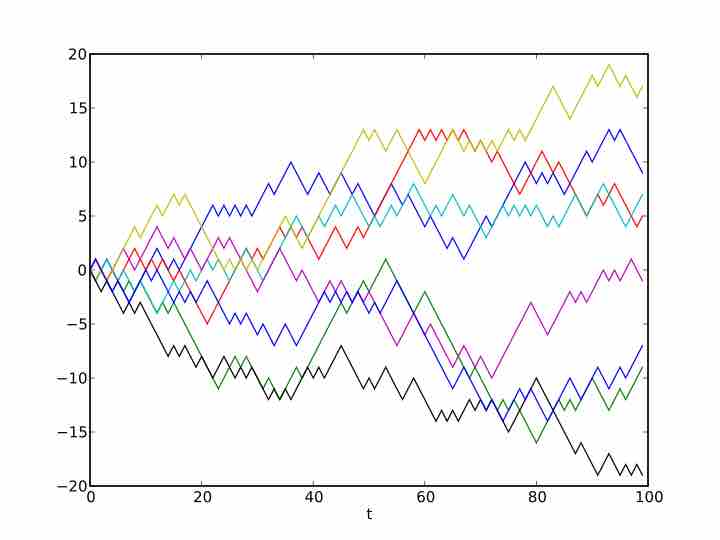
Random Walk
Example of eight random walks in one dimension starting at 0. The plot shows the current position on the line (vertical axis) versus the time steps (horizontal axis).