A Graph of Averages

Linear Regression vs. Graph of Averages

Linear (straight-line) relationships between two quantitative variables are very common in statistics. Often, when we have a scatterplot that shows a linear relationship, we'd like to summarize the overall pattern and make predictions about the data. This can be done by drawing a line through the scatterplot. The regression line drawn through the points describes how the dependent variable $y$ changes with the independent variable $x$. The line is a model that can be used to make predictions, whether it is interpolation or extrapolation. The regression line has the form $y=a+bx$, where $y$ is the dependent variable, $x$ is the independent variable, $b$ is the slope (the amount by which $y$ changes when $x$ increases by one), and $a$ is the $y$-intercept (the value of $y$ when $x=0$).

In most cases, a line will not pass through all points in the data. A good line of regression makes the distances from the points to the line as small as possible. The most common method of doing this is called the "least-squares" method. The least-squares regression line is of the form $\hat{y} = a+bx$, with slope $b = \frac{rs_y}{s_x}$ ($r$ is the correlation coefficient, $s_y$ and $s_x$ are the standard deviations of $y$ and $x$). This line passes through the point $(\bar{x},\bar{y})$ (the means of $x$ and $y$).

Sometimes, a graph of averages is used to show a pattern between the $y$ and $x$ variables. In a graph of averages, the $x$-axis is divided up into intervals. The averages of the $y$ values in those intervals are plotted against the midpoints of the intervals. If we needed to summarize the $y$ values whose $x$ values fall in a certain interval, the point plotted on the graph of averages would be good to use.

The points on a graph of averages do not usually line up in a straight line, making it different from the least-squares regression line. The graph of averages plots a typical $y$ value in each interval: some of the points fall above the least-squares regression line, and some of the points fall below that line.

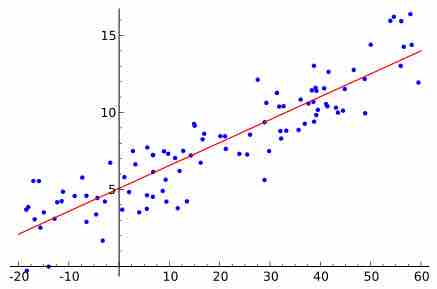
Least Squares Regression Line

Random data points and their linear regression.