In predictive inference, a prediction interval is an estimate of an interval in which future observations will fall, with a certain probability, given what has already been observed. A prediction interval bears the same relationship to a future observation that a frequentist confidence interval or Bayesian credible interval bears to an unobservable population parameter. Prediction intervals predict the distribution of individual future points, whereas confidence intervals and credible intervals of parameters predict the distribution of estimates of the true population mean or other quantity of interest that cannot be observed. Prediction intervals are also present in forecasts; however, some experts have shown that it is difficult to estimate the prediction intervals of forecasts that have contrary series. Prediction intervals are often used in regression analysis.
For example, let's say one makes the parametric assumption that the underlying distribution is a normal distribution and has a sample set
Alternatively, in Bayesian terms, a prediction interval can be described as a credible interval for the variable itself, rather than for a parameter of the distribution thereof.
The concept of prediction intervals need not be restricted to the inference of just a single future sample value but can be extended to more complicated cases. For example, in the context of river flooding, where analyses are often based on annual values of the largest flow within the year, there may be interest in making inferences about the largest flood likely to be experienced within the next 50 years.
Since prediction intervals are only concerned with past and future observations, rather than unobservable population parameters, they are advocated as a better method than confidence intervals by some statisticians.
Prediction Intervals in the Normal Distribution
Given a sample from a normal distribution, whose parameters are unknown, it is possible to give prediction intervals in the frequentist sense -- i.e., an interval
A general technique of frequentist prediction intervals is to find and compute a pivotal quantity of the observables
A prediction interval
where:
the standard score of X, is standard normal distributed. The prediction interval is conventionally written as:
For example, to calculate the 95% prediction interval for a normal distribution with a mean (
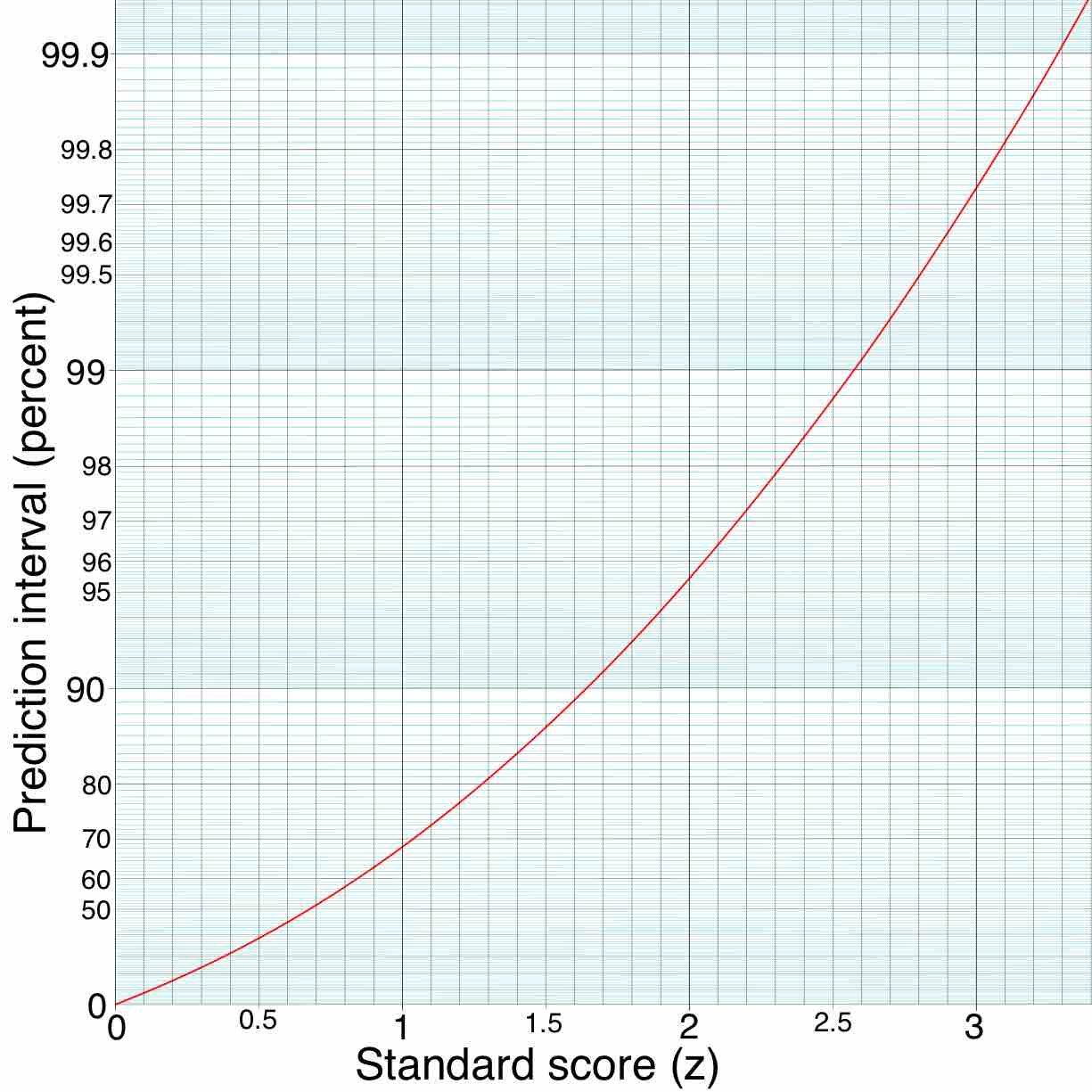
Standard Score and Prediction Interval
Prediction interval (on the