Hypothesis Tests or Confidence Intervals?

What is the difference between hypothesis testing and confidence intervals? When we conduct a hypothesis test, we assume we know the true parameters of interest. When we use confidence intervals, we are estimating the parameters of interest.

Explanation of the Difference

Confidence intervals are closely related to statistical significance testing. For example, if for some estimated parameter $\theta$ one wants to test the null hypothesis that $\theta=0$ against the alternative that $\theta \neq 0$, then this test can be performed by determining whether the confidence interval for $\theta$ contains $0$.

More generally, given the availability of a hypothesis testing procedure that can test the null hypothesis $\theta = \theta_0$ against the alternative that $\theta \neq \theta_0$ for any value of $\theta_0$, then a confidence interval with confidence level $\gamma = 1-\alpha$ can be defined as containing any number $\theta_0$ for which the corresponding null hypothesis is not rejected at significance level $\alpha$.

In consequence, if the estimates of two parameters (for example, the mean values of a variable in two independent groups of objects) have confidence intervals at a given $\gamma$ value that do not overlap, then the difference between the two values is significant at the corresponding value of $\alpha$. However, this test is too conservative. If two confidence intervals overlap, the difference between the two means still may be significantly different.

While the formulations of the notions of confidence intervals and of statistical hypothesis testing are distinct, in some senses and they are related, and are complementary to some extent. While not all confidence intervals are constructed in this way, one general purpose approach is to define a $100(1-\alpha)$% confidence interval to consist of all those values $\theta_0$ for which a test of the hypothesis $\theta = \theta_0$ is not rejected at a significance level of $100 \alpha$%. Such an approach may not always be an option, since it presupposes the practical availability of an appropriate significance test. Naturally, any assumptions required for the significance test would carry over to the confidence intervals.

It may be convenient to say that parameter values within a confidence interval are equivalent to those values that would not be rejected by a hypothesis test, but this would be dangerous. In many instances the confidence intervals that are quoted are only approximately valid, perhaps derived from "plus or minus twice the standard error," and the implications of this for the supposedly corresponding hypothesis tests are usually unknown.

It is worth noting that the confidence interval for a parameter is not the same as the acceptance region of a test for this parameter, as is sometimes assumed. The confidence interval is part of the parameter space, whereas the acceptance region is part of the sample space. For the same reason, the confidence level is not the same as the complementary probability of the level of significance.

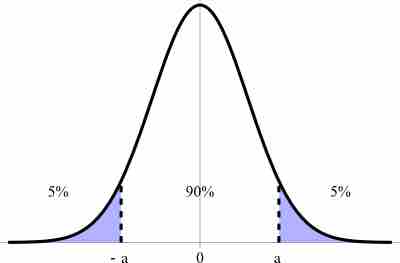
Confidence Interval

This graph illustrates a 90% confidence interval on a standard normal curve.