INTRODUCTION
We have seen a problem-solving strategy with the conservation of energy in the previous section. Here we will adopt the strategy for problems with dissipative forces. Since the work done by nonconservative (or dissipative) forces will irreversibly alter the energy of the system, the total mechanical energy (KE + PE) changes by exactly the amount of work done by nonconservative forces (Wc). Therefore, we obtain
EXAMPLE
Consider the situation shown in , where a baseball player slides to a stop on level ground. Using energy considerations, calculate the distance the 65.0-kg baseball player slides, given that his initial speed is 6.00 m/s and the force of friction against him is a constant 450 N.
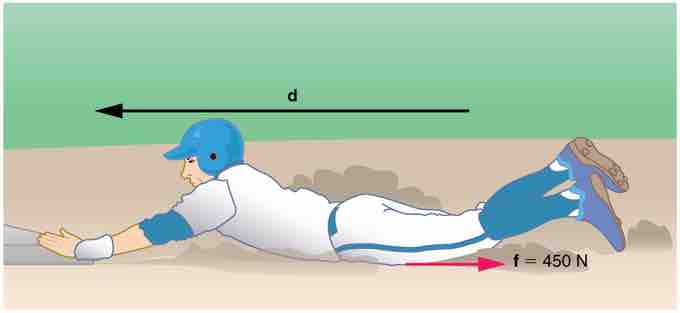
Fig 1
The baseball player slides to a stop in a distance d. In the process, friction removes the player's kinetic energy by doing an amount of work fd equal to the initial kinetic energy.
Strategy: Friction stops the player by converting his kinetic energy into other forms, including thermal energy. In terms of the work-energy theorem, the work done by friction (f), which is negative, is added to the initial kinetic energy to reduce it to zero. The work done by friction is negative, because f is in the opposite direction of the motion (that is, θ=180º, and so cosθ=−1). Thus Wnc=−fd. The equation simplifies to
Solution: Solving the previous equation for d and substituting known values yields, we get d = 2.60 m. The most important point of this example is that the amount of nonconservative work equals the change in mechanical energy.