Reflection and Transmission

When the medium through which a wave travels suddenly changes, the wave often experiences partial transmission and partial refection at the interface. Reflection is a wave phenomenon that changes the direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated. Transmission permits the passage of wave, with some or none of the incident wave being absorbed. Reflection and transmission often occur at the same time .

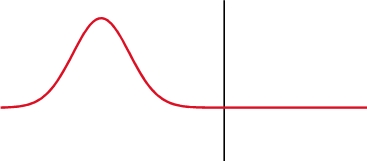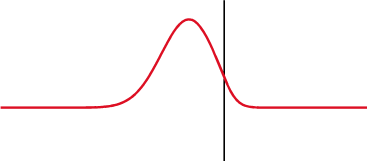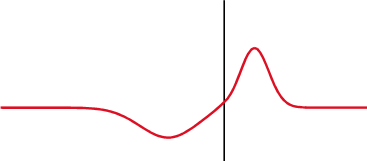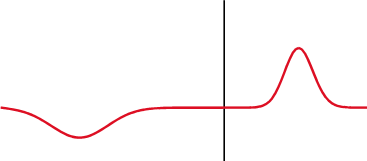
Partial Transmittance and Partial Reflectance

A wave experiences partial transmittance and partial reflectance when the medium through which it travels suddenly changes.

Consider a long string made by connecting two sub-strings with different density $\mu_1, \mu_2$ . When the string is driven by an external force, partial reflection and transmission occurs as in Figure 18426. For the incoming, reflected, and transmitted waves, we can try a solution of the following forms:

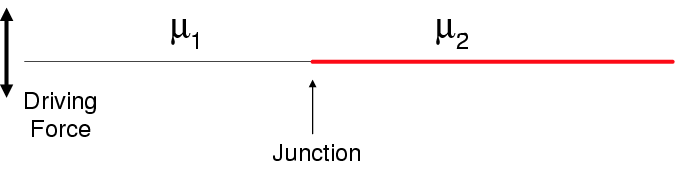
Two Strings With Different Density

Two strings with different density are connected and driven by an external driving force.

$y_{inc} = A ~cos (k_1 x - \omega t) \\ y_{ref} = B~ cos (k_1 x + \omega t)\\ y_{trans} = C ~cos (k_2 x - \omega t)$

k₁ and k₂ are determined by the speed of the wave in each medium. We choose our coordinates such that the junction of two sub-strings is located at x=0. In choosing a trial solution for the waves, we assumed that the incident and transmitted waves travel to the right, while the reflected waves travel to the left. (This is why the '+' sign is chosen before $\omega t$ in the reflected wave. On the left side of the junction, we have

$y_l = y_{inc}+y_{ref} = A~cos(k_1x - \omega t)$.

On the right side, we have

$y_r = y_{trans} = C~cos(k_2 x - \omega t)$.

We will impose additional restriction on the waves by applying "boundary conditions" at x=0. At the boundary x=0, the wave must be continuous and there should be no kinks in it. Thus we must have

$y_l(x=0,t) = y_r(x=0,t)\\ \left ( \frac{\partial y_l(x,t)}{\partial x} \right )_{x=0} = \left ( \frac{\partial y_r(x,t)}{\partial x} \right )_{x=0}$

From the first equation, we get A+B = C. From the second equation, we get A-B = (k₂/k₁)C.

Thus, we get the following result.

$A = \frac{1}{2} (1+\frac{k_2}{k_1})C \\ B = \frac{1}{2} (1-\frac{k_2}{k_1})C \\ $

We can define the transmission (t) and reflection (r) coefficients as

$t = C/A = \frac{2k_1}{k_1+k_2}$, $r = B/A= \frac{k_1-k_2}{k_1+k_2}$.