Harmonic Wave Functions

In this Atom we shall consider wave motion resulting from harmonic vibrations and discuss harmonic transverse wave in the context of a string. We assume there is no loss of energy during transmission of wave along the string. This can be approximated when the string is light and taught. In such condition, if we oscillate the free end in harmonic manner, then the vibrations in the string are simple harmonic motion (SHM), perpendicular to the direction of wave motion. The amplitude of wave form remains intact through its passage along the string.

We know that a traveling wave function representing motion in x-direction has the form:

$y(x,t) = A~f(ax-bt)$.

(Read our Atom on "Mathematical Representation of a Traveling Wave. ") For the case of harmonic vibration, we represent harmonic wave motion in terms of either harmonic sine or cosine function:

$y(x,t) = A~sin(kx -\omega t)$.

Harmonic Oscillatory Properties

Each particle (or a small segment of string) vibrates in SHM. The particle attains the greatest speed at the mean position and reduces to zero at extreme positions. On the other hand, acceleration of the particle is greatest at extreme positions and zero at the mean position. The vibration of particle is represented by a harmonic sine or cosine function. For x=0:

$y(x=0,t) = A~sin(\omega t)=A~sin(\omega t)$.

Clearly, the displacement in y-direction is described by the bounded sine or cosine function. The important point here is to realize that oscillatory attributes (like time period, angular and linear frequency) of wave motion is same as that of vibration of a particle in transverse direction.

We know that time period in SHM is equal to time taken by the particle to complete one oscillation. It means that displacement of the particle from the mean position at a given position such as x=0 has same value after time period "T" for:

$\omega T = 2\pi$. Therefore, $\omega = \frac{2\pi}{T}$.

Similarly, displacement of the particle from the mean position at a given time such as t=0 has same value by change the position by " , where $k \lambda = 2 \pi$. k is called wavenumber.

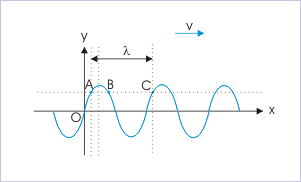
Harmonic Waves

Harmonic waves are described by sinusoidal functions. The wavelength is equal to linear distance between repetitions of transverse disturbance or phase.

We can determine speed of the wave by noting that wave travels a linear distance " in one period (T). Thus, speed of wave is given by :

$v = \frac{\lambda}{T} = \frac{\omega}{k}$.