Simple Harmonic Motion

Simple Harmonic Motion

Simple harmonic motion is a type of periodic motion where the restoring force is directly proportional to the displacement (i.e., it follows Hooke's Law) . It can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. In addition, other phenomena can be approximated by simple harmonic motion, such as the motion of a simple pendulum, or molecular vibration.

Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. A system that follows simple harmonic motion is known as a simple harmonic oscillator.

Dynamics of Simple Harmonic Oscillation

For one-dimensional simple harmonic motion, the equation of motion (which is a second-order linear ordinary differential equation with constant coefficients) can be obtained by means of Newton's second law and Hooke's law.

$F_{net}=m\frac{d^{2}x}{dt^{2}}=-kx$,

where m is the mass of the oscillating body, x is its displacement from the equilibrium position, and k is the spring constant. Therefore:

$\frac{d^{2}x}{dt^{2}}=-(\frac{k}{m})x$.

Solving the differential equation above, a solution which is a sinusoidal function is obtained.

$x(t)=c_{1}cos(\omega t)+c_{2}sin(\omega t)=Acos(\omega t - \varphi )$,

where

$\omega = \sqrt{\frac{k}{m}}$,

$A=\sqrt{c_{1}^{2}+c_{2}^{2}}$,

$tan\varphi=(\frac{c_{2}}{c_{1}})$.

In the solution, c₁ and c₂ are two constants determined by the initial conditions, and the origin is set to be the equilibrium position. Each of these constants carries a physical meaning of the motion: A is the amplitude (maximum displacement from the equilibrium position), ω = 2πf is the angular frequency, and φ is the phase.

We can use differential calculus and find the velocity and acceleration as a function of time:

$v(t)=\frac{dx}{dt}=-A\omega sin(\omega t-\varphi )$

$a(t)=\frac{d^{2}x}{dt^{2}}=-A\omega ^{2}cos(\omega t-\varphi )$.

Acceleration can also be expressed as a function of displacement:

$a(t)=-\omega ^{2}x$.

Then since ω = 2πf,

$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$.

Recalling that $T=1/f$,

$T=2\pi \sqrt{\frac{m}{k}}$.

Using Newton's Second Law, Hooke's Law, and some differential Calculus, we were able to derive the period and frequency of the mass oscillating on a spring that we encountered in the last section! Note that the period and frequency are completely independent of the amplitude.

The below figure shows the simple harmonic motion of an object on a spring and presents graphs of x(t),v(t), and a(t) versus time. You should learn to create mental connections between the above equations, the different positions of the object on a spring in the cartoon, and the associated positions in the graphs of x(t), v(t), and a(t) .

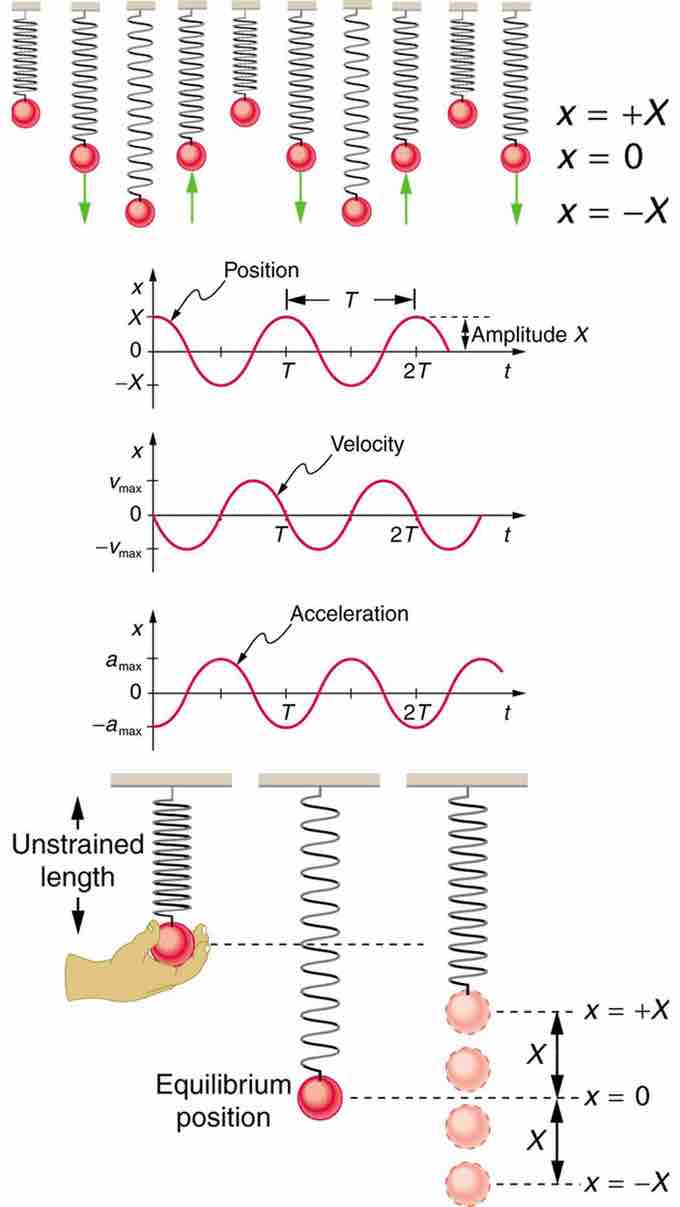
Visualizing Simple Harmonic Motion

Graphs of x(t),v(t), and a(t) versus t for the motion of an object on a spring. The net force on the object can be described by Hooke's law, and so the object undergoes simple harmonic motion. Note that the initial position has the vertical displacement at its maximum value X; v is initially zero and then negative as the object moves down; and the initial acceleration is negative, back toward the equilibrium position and becoming zero at that point.