Newton's Rings
In 1717, Isaac Newton first analyzed an interference pattern caused by the reflection of light between a spherical surface and an adjacent flat surface. Although first observed by Robert Hooke in 1664, this pattern is called Newton's rings, as Newton was the first to analyze and explain the phenomena. Newton's rings appear as a series of concentric circles centered at the point of contact between the spherical and flat surfaces. When viewed with monochromatic light, Newton's rings appear as alternating bright and dark rings; when viewed with white light, a concentric ring pattern of rainbow colors is observed. An example of Newton's rings when viewed with white light is shown in the figure below .

Newton's Rings in a drop of water
Newton's rings seen in two plano-convex lenses with their flat surfaces in contact. One surface is slightly convex, creating the rings. In white light, the rings are rainbow-colored, because the different wavelengths of each color interfere at different locations.
The light rings are caused by constructive interference between the light rays reflected from both surfaces, while the dark rings are caused by destructive interference. The outer rings are spaced more closely than the inner ones because the slope of the curved lens surface increases outwards. The radius of the Nth bright ring is given by:
where N is the bright-ring number, R is the radius of curvature of the lens the light is passing through, and λ is the wavelength of the light passing through the glass.
A spherical lens is placed on top of a flat glass surface. An incident ray of light passes through the curved lens until it comes to the glass-air boundary, at which point it passes from a region of higher refractive index n (the glass) to a region of lower n (air). At this boundary, some light is transmitted into the air, while some light is reflected. The light that is transmitted into the air does not experience a change in phase and travels a a distance, d, before it is reflected at the flat glass surface below. This second air-glass boundary imparts a half-cycle phase shift to the reflected light ray because air has a lower n than the glass. The two reflected light rays now travel in the same direction to be detected. As one gets farther from the point at which the two surfaces touch, the distance d increases because the lens is curving away from the flat surface .
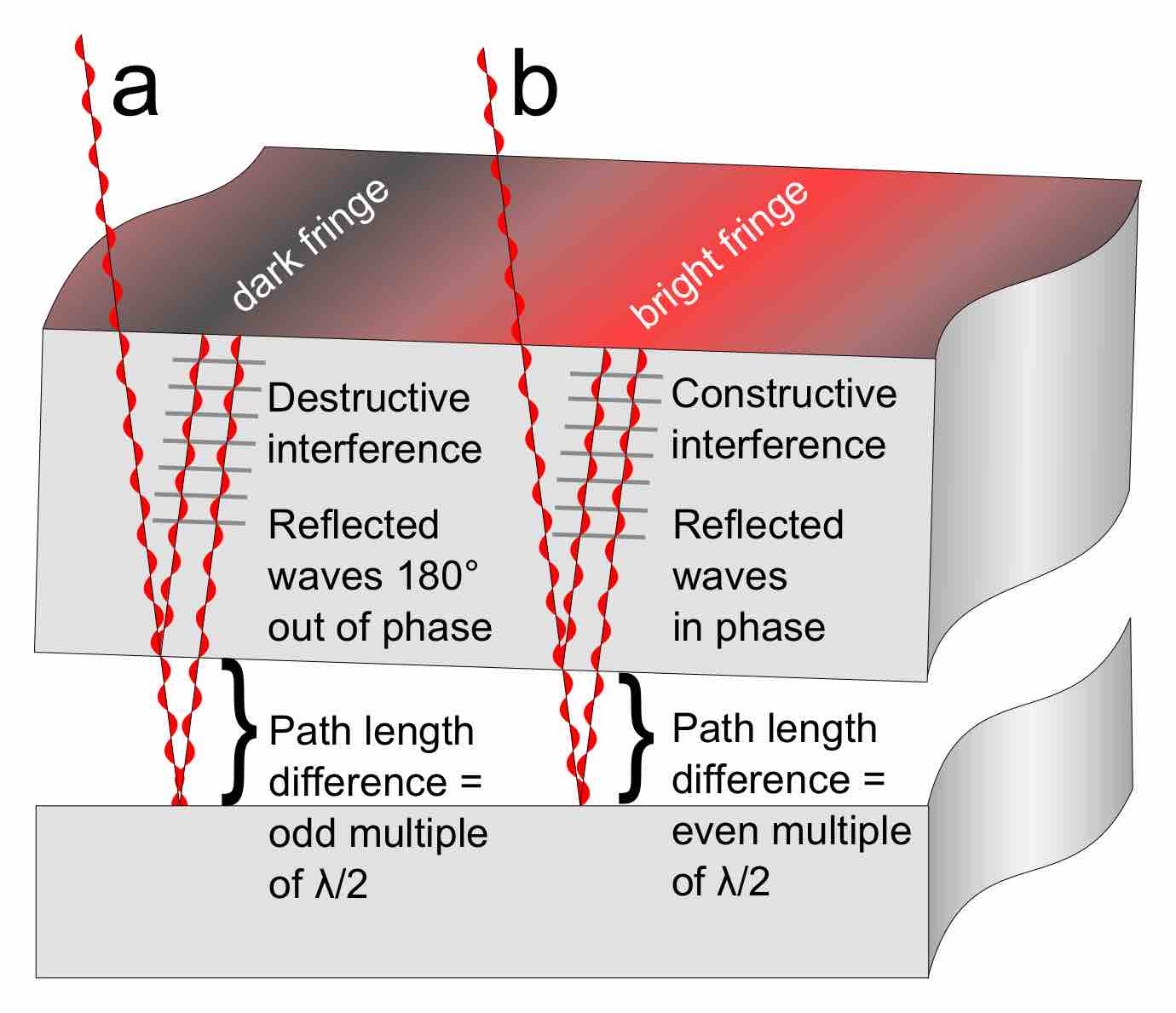
Formation of Interference Fringes
This figure shows how interference fringes form.
If the path length difference between the two reflected light beams is an odd multiple of the wavelength divided by two, λ/2, the reflected waves will be 180 degrees out of phase and destructively interfere, causing a dark fringe. If the path-length difference is an even multiple of λ/2, the reflected waves will be in phase with one another. The constructive interference of the two reflected waves creates a bright fringe.