Conditions for Wave Interference: Reflection due to Phase Change

Conditions for Wave Interference

Interference is a phenomenon in which two waves superimpose to form a resultant wave of greater or lesser amplitude. Its effects can be observed in all types of waves (for example, light, acoustic waves and water waves). Interference usually refers to the interaction of waves that are correlated (coherent) with each other because they originate from the same source, or they have the same or nearly the same frequency. When two or more waves are incident on the same point, the total displacement at that point is equal to the vector sum of the displacements of the individual waves. If a crest of one wave meets a crest of another wave of the same frequency at the same point, then the magnitude of the displacement is the sum of the individual magnitudes. This is constructive interference and occurs when the phase difference between the waves is a multiple of 2π. Destructive interference occurs when the crest of one wave meets a trough of another wave. In this case, the magnitude of the displacements is equal to the difference in the individual magnitudes, and occurs when this difference is an odd multiple of π. Examples of constructive and destructive interference are shown in . If the difference between the phases is intermediate between these two extremes, then the magnitude of the displacement of the summed waves lies between the minimum and maximum values.

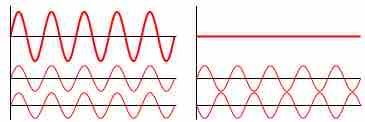
Wave Interference

Examples of constructive (left) and destructive (right) wave interference.

A simple form of wave interference is observed when two waves of the same frequency (also called a plane wave) intersect at an angle , as shown in . Assuming the two waves are in phase at point B, then the relative phase changes along the x-axis. The phase difference at point A is given by:

Interference of Plane Waves

Geometrical arrangement for two plane wave interference.

$\Delta \varphi = \frac{2 \pi d}{\lambda} = \frac{2 \pi x sin \theta}{\lambda}$

Constructive interference occurs when the waves are in phase, or

$\frac{x sin \theta}{\lambda} = 0, \pm 1, \pm 2, ...$

Destructive interference occurs when the waves are half a cycle out of phase, or

$\frac{x sin \theta}{\lambda} = \pm \frac{1}{2}, \pm \frac{3}{2} , ...$

Reflection Due to Phase Change

Light exhibits wave characteristics in various media as well as in a vacuum. When light goes from a vacuum to some medium (like water) its speed and wavelength change, but its frequency f remains the same. The speed of light in a medium is v = c/n, where n is the index of refraction. For example, water has an index of refraction of n = 1.333. When light is reflected off a medium with a higher index of refraction, crests get reflected as troughs and troughs get reflected as crests. In other words, the wave undergoes a 180 degree change of phase upon reflection, and the reflected ray "jumps" ahead by half a wavelength.