Universal Gravitation for Spherically Symmetric Bodies

The Law of Universal Gravitation states that the gravitational force between two points of mass is proportional to the magnitudes of their masses and the inverse-square of their separation, $d$:

$\displaystyle F=\frac{GmM}{d^2}$

However, most objects are not point particles. Finding the gravitational force between three-dimensional objects requires treating them as points in space. For highly symmetric shapes such as spheres or spherical shells, finding this point is simple.

The Shell Theorem

Isaac Newton proved the Shell Theorem, which states that:

1. A spherically symmetric object affects other objects gravitationally as if all of its mass were concentrated at its center,
2. If the object is a spherically symmetric shell (i.e., a hollow ball) then the net gravitational force on a body inside of it is zero.

Since force is a vector quantity, the vector summation of all parts of the shell/sphere contribute to the net force, and this net force is the equivalent of one force measurement taken from the sphere's midpoint, or center of mass (COM). So when finding the force of gravity exerted on a ball of 10 kg, the distance measured from the ball is taken from the ball's center of mass to the earth's center of mass.

Given that a sphere can be thought of as a collection of infinitesimally thin, concentric, spherical shells (like the layers of an onion), then it can be shown that a corollary of the Shell Theorem is that the force exerted in an object inside of a solid sphere is only dependent on the mass of the sphere inside of the radius at which the object is. That is because shells at a greater radius than the one at which the object is, do not contribute a force to an object inside of them (Statement 2 of theorem).

When considering the gravitational force exerted on an object at a point inside or outside a uniform spherically symmetric object of radius $R$, there are two simple and distinct situations that must be examined: the case of a hollow spherical shell, and that of a solid sphere with uniformly distributed mass.

Case 1: A hollow spherical shell

The gravitational force acting by a spherically symmetric shell upon a point mass inside it, is the vector sum of gravitational forces acted by each part of the shell, and this vector sum is equal to zero. That is, a mass $m$ within a spherically symmetric shell of mass $M$, will feel no net force (Statement 2 of Shell Theorem).

The net gravitational force that a spherical shell of mass $M$ exerts on a body outside of it, is the vector sum of the gravitational forces acted by each part of the shell on the outside object, which add up to a net force acting as if mass $M$ is concentrated on a point at the center of the sphere (Statement 1 of Shell Theorem).

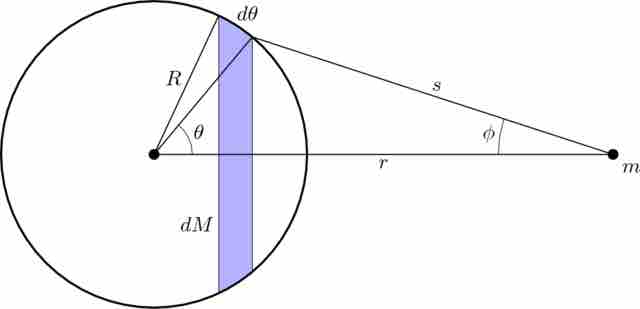
Diagram used in the proof of the Shell Theorem

This diagram outlines the geometry considered when proving The Shell Theorem. In particular, in this case a spherical shell of mass $M$ (left side of figure) exerts a force on mass $m$ (right side of the figure) outside of it. The surface area of a thin slice of the sphere is shown in color. (Note: The proof of the theorem is not presented here. Interested readers can explore further using the sources listed at the bottom of this article.)

Case 2: A solid, uniform sphere

The second situation we will examine is for a solid, uniform sphere of mass $M$ and radius $R$, exerting a force on a body of mass $m$ at a radius $d$ inside of it (that is, $d< R$). We can use the results and corollaries of the Shell Theorem to analyze this case. The contribution of all shells of the sphere at a radius (or distance) greater than $d$ from the sphere's center-of-mass can be ignored (see above corollary of the Shell Theorem). Only the mass of the sphere within the desired radius $M_{<d}$(that is the mass of the sphere inside $d$) is relevant, and can be considered as a point mass at the center of the sphere. So, the gravitational force acting upon point mass $m$ is:

$\displaystyle F=\frac{GmM_{<d}}{d^2}$

where it can be shown that $\displaystyle M_{<d}=\frac{4}{3}\pi d^3 \rho$

($\rho$ is the mass density of the sphere and we are assuming that it does not depend on the radius. That is, the sphere's mass is uniformly distributed.)

Therefore, combining the above two equations we get:

$F=\frac{4}{3} \pi Gm \rho d$

which shows that mass $m$ feels a force that is linearly proportional to its distance, $d$, from the sphere's center of mass.

As in the case of hollow spherical shells, the net gravitational force that a solid sphere of uniformly distributed mass $M$ exerts on a body outside of it, is the vector sum of the gravitational forces acted by each shell of the sphere on the outside object. The resulting net gravitational force acts as if mass $M$ is concentrated on a point at the center of the sphere, which is the center of mass, or COM (Statement 1 of Shell Theorem). More generally, this result is true even if the mass $M$ is not uniformly distributed, but its density varies radially (as is the case for planets).