Kepler's First Law

Kepler's First Law

Kepler's first law states that

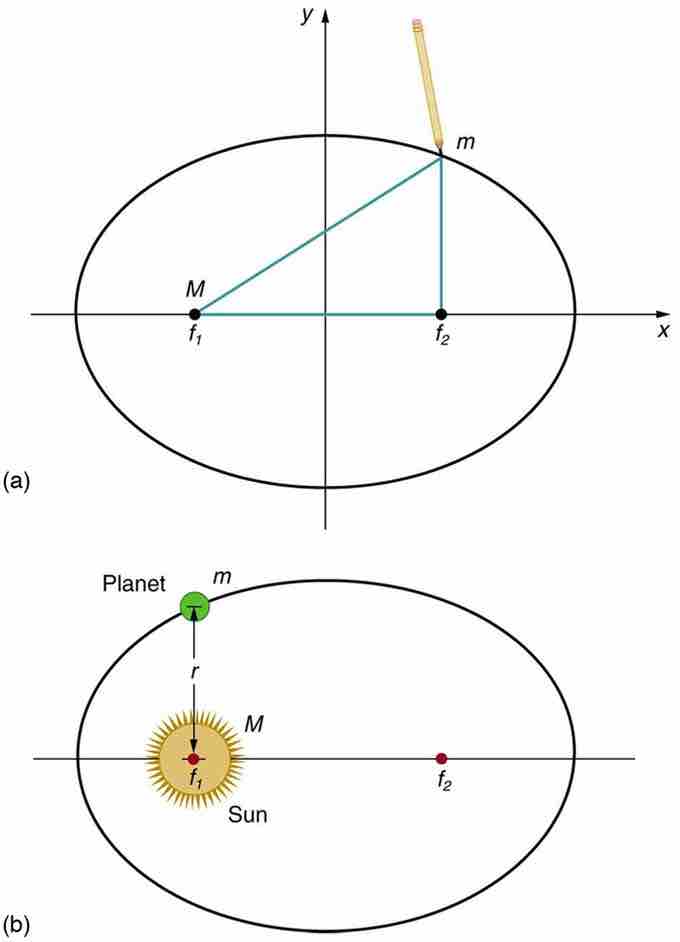
The orbit of every planet is an ellipse with the Sun at one of the two foci.

An ellipse is a closed plane curve that resembles a stretched out circle. Note that the Sun is not at the center of the ellipse, but at one of its foci. The other focal point, $f_2$, has no physical significance for the orbit. The center of an ellipse is the midpoint of the line segment joining its focal points. A circle is a special case of an ellipse where both focal points coincide.

Ellipses and Kepler's First Law

(a) An ellipse is a closed curve such that the sum of the distances from a point on the curve to the two foci ($f_1$ and $f_2$) is a constant. You can draw an ellipse as shown by putting a pin at each focus, and then placing a string around a pencil and the pins and tracing a line on paper. A circle is a special case of an ellipse in which the two foci coincide (thus any point on the circle is the same distance from the center). (b) For any closed gravitational orbit, $m$ follows an elliptical path with $M$ at one focus. Kepler's first law states this fact for planets orbiting the Sun.

How stretched out an ellipse is from a perfect circle is known as its eccentricity: a parameter that can take any value greater than or equal to 0 (a circle) and less than 1 (as the eccentricity tends to 1, the ellipse tends to a parabola). The eccentricities of the planets known to Kepler varied from 0.007 (Venus) to 0.2 (Mercury). Minor bodies such as comets an asteroids (discovered after Kepler's time) can have very large eccentricities. The dwarf planet Pluto, discovered in 1929, has an eccentricity of 0.25.

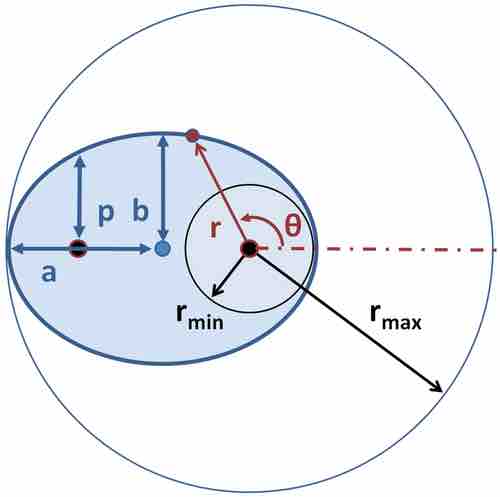
Symbolically, an ellipse can be represented in polar coordinates as:

$\displaystyle r=\frac{p}{1+ \epsilon \cos \theta }$

where $(r, \theta)$ are the polar coordinates (from the focus) for the ellipse, $p$ is the semi-latus rectum, and $\epsilon$ is the eccentricity of the ellipse. For a planet orbiting the Sun, $r$ is the distance from the Sun to the planet and $\theta$ is the angle between the planet's current position and its closest approach, with the Sun as the vertex.

Orbit As Ellipse

Heliocentric coordinate system $(r, \theta)$ for ellipse. Also shown are: semi-major axis $a$, semi-minor axis $b$ and semi-latus rectum $p$; center of ellipse and its two foci marked by large dots. For $\theta = 0$°, $r = r_{\text{min}}$ and for $\theta = 180$°, $r= r_{\text{max}}$.

At $\theta = 0$°, perihelion, the distance is minimum

$\displaystyle r_{\text{min}}=\frac{p}{1+ \epsilon}$.

At $\theta = 90$° and at $\theta = 270$°, the distance is $p$.

At $\theta = 180$°, aphelion, the distance is maximum

$\displaystyle r_{\text{max}}=\frac{p}{1-\epsilon}$.

The semi-major axis $a$ is the arithmetic mean between $r_{\text{min}}$ and $r_{\text{max}}$:

$r_{max}-a=a-r_{min}$

$\displaystyle a=\frac{p}{1-\epsilon^{2}}$.

The semi-minor axis $b$ is the geometric mean between $r_{\text{min}}$ and $r_{\text{max}}$:

$\displaystyle \frac{r_{max}}{b}=\frac{b}{r_{min}}$

$\displaystyle b=\frac{p}{\sqrt{1-\epsilon^{2}}}$

The semi-latus rectum $p$ is the harmonic mean between $r_{\text{min}}$ and $r_{\text{max}}$:

$\displaystyle \frac{1}{r_{min}}-\frac{1}{p}=\frac{1}{p}-\frac{1}{r_{max}}$

$\displaystyle pa=r_{max}\cdot r_{min}=b^{2}$.

The eccentricity $\epsilon$ is the coefficient of variation between $r_{\text{min}}$ and $r_{\text{max}}$:

$\displaystyle \epsilon=\frac{r_{\text{max}}-r_{\text{min}}}{r_{\text{max}}+r_{\text{min}}}$

The area of the ellipse is

$A=\pi ab$

The special case of a circle is $\epsilon = 0$, resulting in $r = p = r_{\text{min}} = r_{\text{max}} = a = b $ and $A = \pi r^2$. The orbits of planets with very small eccentricities can be approximated as circles.