The Third Law

The third law of thermodynamics is sometimes stated as follows: The entropy of a perfect crystal at absolute zero is exactly equal to zero.

At zero kelvin the system must be in a state with the minimum possible energy, thus this statement of the third law holds true if the perfect crystal has only one minimum energy state. Entropy is related to the number of possible microstates, and with only one microstate available at zero kelvin the entropy is exactly zero.

The third law was developed by the chemist Walther Nernst during the years 1906-1912. It is often referred to as Nernst's theorem or Nernst's postulate. Nernst proposed that the entropy of a system at absolute zero would be a well-defined constant. Instead of being 0, entropy at absolute zero could be a nonzero constant, due to the fact that a system may have degeneracy (having several ground states at the same energy).

In simple terms, the third law states that the entropy of a perfect crystal approaches zero as the absolute temperature approaches zero. This law provides an absolute reference point for the determination of entropy. ( diagrams the temperature entropy of nitrogen. ) The entropy (S) determined relative to this point is the absolute entropy represented as follows:

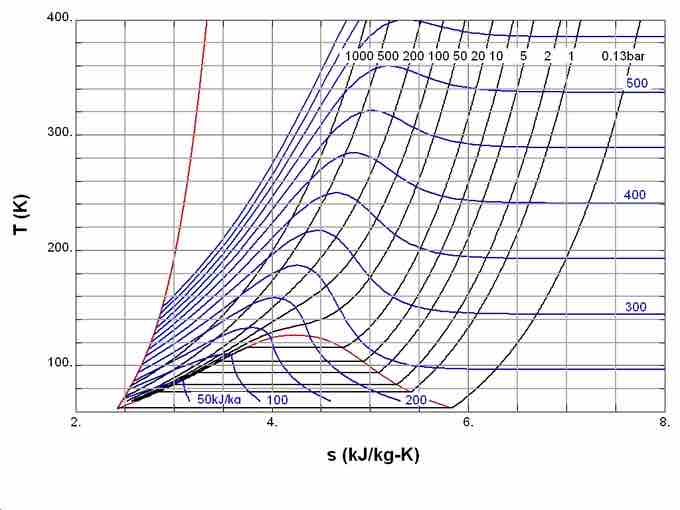
Temperature Entropy of Nitrogen

Temperature–entropy diagram of nitrogen. The red curve at the left is the melting curve. Absolute value of entropy can be determined shown here, thanks to the third law of thermodynamics.

$S = k_B logW$,

where k_B is the Bolzmann constant and W is the number of microstates. Provided that the ground state is unique (or W=1), the entropy of a perfect crystal lattice as defined by Nernst's theorem is zero provided that its ground state is unique, because log(1) = 0.