Overview
The normal force,
A common situation in which a normal force exists is when a person stands on the ground. Because of Newton's third law, the ground exerts a force on the person that is equal in magnitude to the person's weight. In this simple case, the weight of the person and the opposing normal force are the only two forces considered on the person. The person remains still because the forces due to weight and the normal force create a net force of zero on the person.
Forces on Inclined Planes
A more complex example of a situation in which a normal force exists is when a mass rests on an inclined plane. In this case, the normal force is not in the exact opposite direction as the force due to the weight of the mass. This is because the mass contacts the surface at an angle. By taking this angle into account, the magnitude of the normal force (
where:
-
$m$ is the mass under consideration, -
$g$ is the acceleration due to gravity, - and
$\theta$ is the angle between the inclined surface and the horizontal.
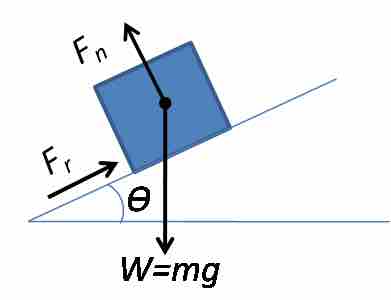
Inclined Plane
A mass rests on an inclined plane that is at an angle
Another interesting example involving normal forces is when a person stands in an elevator. When the elevator goes up, the normal force is actually greater than the force due to gravity. In this situation there are only two forces acting on the person. The first is the force of gravity on the person, which does not change. The second is the normal force. By summing the forces and setting them equal to
where:
-
$F_N$ is the normal force, -
$m \cdot g$ is the force due to gravity, -
$m$ is the mass of the person, - and
$a$ is the acceleration.
Since acceleration is positive, the normal force must actually be greater than the force due to gravity (the weight of the person).