Overview
A moving object in a viscous fluid is equivalent to a stationary object in a flowing fluid stream. (For example, when you ride a bicycle at 10 m/s in still air, you feel the air in your face exactly as if you were stationary in a 10-m/s wind. ) Flow of the stationary fluid around a moving object may be laminar, turbulent, or a combination of the two. Just as with flow in tubes, it is possible to predict when a moving object creates turbulence. We use another form of the Reynolds number N′R, defined for an object moving in a fluid to be
where L is a characteristic length of the object (a sphere's diameter, for example), the fluid density, its viscosity, and v the object's speed in the fluid. If N′R is less than about 1, flow around the object can be laminar, particularly if the object has a smooth shape. The transition to turbulent flow occurs for N′R between 1 and about 10, depending on surface roughness and so on. Depending on the surface, there can be a turbulent wake behind the object with some laminar flow over its surface. For an N′R between 10 and 10^6, the flow may be either laminar or turbulent and may oscillate between the two. For N′R greater than about 10^6, the flow is entirely turbulent, even at the surface of the object. (See . ) Laminar flow occurs mostly when the objects in the fluid are small, such as raindrops, pollen, and blood cells in plasma.
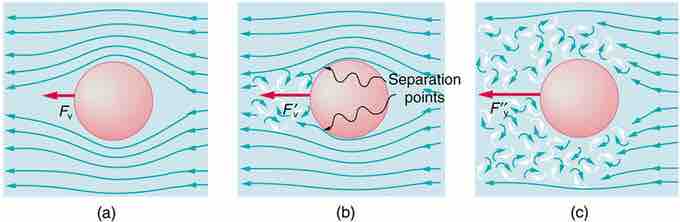
Motion of an object in a viscous fluid.
(a) Motion of this sphere to the right is equivalent to fluid flow to the left. Here the flow is laminar with N′R less than 1. There is a force, called viscous drag FV, to the left on the ball due to the fluid's viscosity. (b) At a higher speed, the flow becomes partially turbulent, creating a wake starting where the flow lines separate from the surface. Pressure in the wake is less than in front of the sphere, because fluid speed is less, creating a net force to the left F′V that is significantly greater than for laminar flow. Here N′R is greater than 10. (c) At much higher speeds, where N′R is greater than 10^6, flow becomes turbulent everywhere on the surface and behind the sphere. Drag increases dramatically.
Viscous Drag
One of the consequences of viscosity is a resistance force called viscous drag