As vector fields, electric fields obey the superposition principle. This principle states that for all linear systems, the net response to multiple stimuli at a given place and time is equal to the sum of the responses that would have resulted from each stimulus individually.
Possible stimuli include but are not limited to: numbers, functions, vectors, vector fields, and time-varying signals. It should be noted that the superposition principle is applicable to any linear system, including algebraic equations, linear differential equations, and systems of equations of the aforementioned forms.
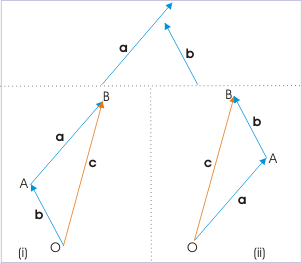
For example, if forces A and B are constant and simultaneously act upon an object, illustrated as O in , the resultant force will be the sum of forces A and B. Vector addition is commutative, so whether adding A to B or B to A makes no difference on the resultant vector; this is also the case for subtraction of vectors.
Vector addition
Forces a and b act upon an object at point O. Their sum is commutative, and results in a resultant vector c.
Electric fields are continuous fields of vectors, so at a given point, one can find the forces that several fields will apply to a test charge and add them to find the resultant. To do this, first find the component vectors of force applied by each field in each of the orthogonal axes. This can be done using trigonometric functions. Then once the component vectors are found, add the components in each axis that are applied by the combined electric fields.
This is one only form of solution. An overall resultant vector can be found by using the Pythagorean theorem to find the resultant (the hypotenuse of the triangle created with applied forces as legs) and the angle with respect to a given axis by equating the inverse tangent of the angle to the ratio of the forces of the adjacent and opposite legs.