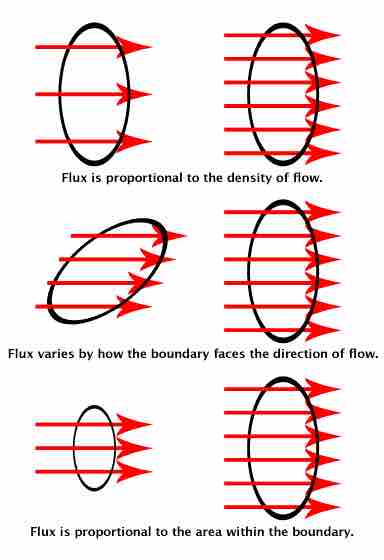
Electric Flux

Electric flux is the rate of flow of the electric field through a given area (see ). Electric flux is proportional to the number of electric field lines going through a virtual surface.

Electric Flux

Electric flux visualized. The ring shows the surface boundaries. The red arrows for the electric field lines.

If the electric field is uniform, the electric flux passing through a surface of vector area S is $\Phi_E = \mathbf{E} \cdot \mathbf{S} = ES \cos \theta$ where E is the magnitude of the electric field (having units of V/m), S is the area of the surface, and θ is the angle between the electric field lines and the normal (perpendicular) to S.

For a non-uniform electric field, the electric flux dΦE through a small surface area dS is given by $d\Phi_E = \mathbf{E} \cdot d\mathbf{S}$ (the electric field, E, multiplied by the component of area perpendicular to the field).

Gauss' Law describes the electric flux over a surface S as the surface integral: $\Phi_E = \iint_S \mathbf{E} \cdot d\mathbf{S}$ where E is the electric field and dS is a differential area on the closed surface S with an outward facing surface normal defining its direction.

It is important to note that while the electric flux is not affected by charges that are not within the closed surface, the net electric field, E, in the Gauss' Law equation, can be affected by charges that lie outside the closed surface. While Gauss' Law holds for all situations, it is only useful for "by hand" calculations when high degrees of symmetry exist in the electric field. Examples include spherical and cylindrical symmetry.

Electric flux has SI units of volt metres (V m), or, equivalently, newton metres squared per coulomb (N m² C⁻¹). Thus, the SI base units of electric flux are kg·m³·s⁻³·A⁻¹.