Solving Problems with Vectors and Coulomb's Law

Solving Problems with Vectors and Coulomb's Law

Electric Force Between Two Point Charges

To address the electrostatic forces among electrically charged particles, first consider two particles with electric charges q and Q , separated in empty space by a distance r. Suppose that we want to find the electric force vector on charge q. (The electric force vector has both a magnitude and a direction. ) We can express the location of charge q as r_q, and the location of charge Q as r_Q. In this way we can know both how strong the electric force is on a charge, but also what direction that force is directed in. Coulomb's Law using vectors can be written as:

$\mathbf{F_E} = \frac{kqQ(\mathbf{r}_q - \mathbf{r}_Q)}{|\mathbf{r}_q - \mathbf{r}_Q|^3}$

In this equation, k is equal to $\frac{1}{4\pi\varepsilon_0\varepsilon }$,where $\varepsilon_0$ is the permittivity of free space and $\varepsilon$ is the relative permittivity of the material in which the charges are immersed. The variables $\mathbf{F_E}$, $\mathbf{r}_q$, and $\mathbf{r}_Q$are in bold because they are vectors. Thus, we need to find $\mathbf{r}_q - \mathbf{r}_Q$ by performing standard vector subtraction. This means that we need to subtract the corresponding components of vector $\mathbf{r}_Q$ from vector $\mathbf{r}_q$.

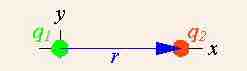
This vector notation can be used in the simple example of two point charges where only one of which is a source of charge .

Application of Coulomb's Law

In a simple example, the vector notation of Coulomb's Law can be used when there are two point charges and only one of which is a source charge.

Electric Force on a Field Charge Due to Fixed Source Charges

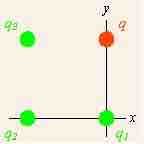
Suppose there is more than one point source charges providing forces on a field charge. diagrams a fairly simple example with three source charges (shown in green and indexed by subscripts) and one field charge (in red, designated q). We assume that the source charges are fixed in space, and the field charge q is subject to forces from the source charges.

Multiple point charges

Coulomb's Law applied to more than one point source charges providing forces on a field charge.

Note the coordinate system that has been chosen. All of the charges lie on the corners of a square, and the origin is chosen to collocate with the lower right source charge, and aligned with the square. Since we can have only one origin of coordinates, no more than one of the source points can lie at the origin, and the displacements from different source points to the field point differ. The total force on the field charge q is due to applications of the force described in the vector notation of Coulomb's Law from each of the source charges. The total force is therefore the sum of these individual forces .

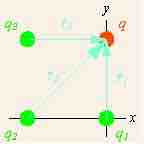
Displacements of field charge

The displacements of the field charge from each source charge are shown as light blue arrows.

Applying Coulomb's Law three times and summing the results gives us:

$\mathbf{F_{E_q}} = \frac{kq\cdot q_1(\mathbf{r}_q - \mathbf{r}_{q1})}{|\mathbf{r}_q - \mathbf{r}_{q1}|^3} + \frac{kq\cdot q_2(\mathbf{r}_q - \mathbf{r}_{q2})}{|\mathbf{r}_q - \mathbf{r}_{q2}|^3} +\frac{kq\cdot q_3(\mathbf{r}_q - \mathbf{r}_{q3})}{|\mathbf{r}_q - \mathbf{r}_{q3}|^3}$.

This equation can further be simplified and applied to a fixed number of charge points.

$\mathbf{F_n} = \sum_{i \ne n} \frac{q_n q_i(\mathbf{r}_n - \mathbf{r}_i)}{4 \pi \epsilon_0|\mathbf{r}_n - \mathbf{r}_i|^3}$