The Integral Test and Estimates of Sums

The integral test for convergence is a method used to test infinite series of non-negative terms for convergence. It was developed by Colin Maclaurin and Augustin-Louis Cauchy and is sometimes known as the Maclaurin–Cauchy test.

Statement of the test

Consider an integer $N$ and a non-negative function $f$ defined on the unbounded interval $[N, \infty )$, on which it is monotonically decreasing. The infinite series $\sum_{n=N}^\infty f(n)$ converges to a real number if and only if the improper integral $\int_N^\infty f(x)\,dx$ is finite. In other words, if the integral diverges, then the series diverges as well.

Although we won't go into the details, the proof of the test also gives the lower and upper bounds:

$\displaystyle{\int_N^\infty f(x)\,dx\le\sum_{n=N}^\infty f(n)\le f(N)+\int_N^\infty f(x)\,dx}$

for the infinite series.

Applications

The harmonic series $\sum_{n=1}^\infty \frac1n$ diverges because, using the natural logarithm (its derivative) and the fundamental theorem of calculus, we get:

$\displaystyle{\int_1^M\frac1x\,dx=\ln x\Bigr|_1^M=\ln M\to\infty \quad\text{for }M\to\infty}$

On the other hand, the series $\sum_{n=1}^\infty \frac1{n^{1+\varepsilon}}$ converges for every $\varepsilon > 0$ because, by the power rule:

 $\displaystyle{\int_1^M\frac1{x^{1+\varepsilon}}\,dx =-\frac1{\varepsilon x^\varepsilon}\biggr|_1^M= \frac1\varepsilon\Bigl(1-\frac1{M^\varepsilon}\Bigr) \le\frac1\varepsilon }$

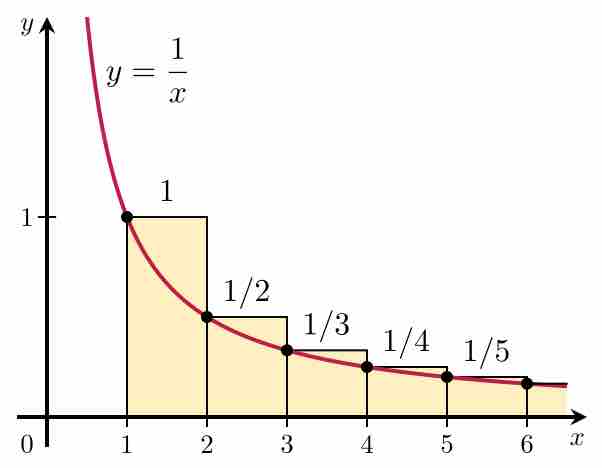
Integral Test

The integral test applied to the harmonic series. Since the area under the curve $y = \frac{1}{x}$ for $x \in [1, \infty)$ is infinite, the total area of the rectangles must be infinite as well.

The above examples involving the harmonic series raise the question of whether there are monotone sequences such that $f(n)$ decreases to $0$ faster than $\frac{1}{n}$but slower than $\frac{1}{n^{1 + \varepsilon}}$ in the sense that:

$\displaystyle{\lim_{n\to\infty}\frac{f(n)}{\frac{1}{n}}=0}$

and:

$\displaystyle{\lim_{n\to\infty}\frac{f(n)}{\frac{1}{n^{1+\varepsilon}}}=\infty}$

for every $\varepsilon > 0$, and whether the corresponding series of the $f(n)$ still diverges. Once such a sequence is found, a similar question can be asked of $f(n)$ taking the role of $\frac{1}{n}$ oand so on. In this way, it is possible to investigate the borderline between divergence and convergence of infinite series.