A Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point. The concept of a Taylor series was formally introduced by the English mathematician Brook Taylor in 1715. If the Taylor series is centered at zero, then that series is also called a Maclaurin series, named after the Scottish mathematician Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.
It is common practice to approximate a function by using a finite number of terms of its Taylor series. Taylor's theorem gives quantitative estimates on the error in this approximation. Any finite number of initial terms of the Taylor series of a function is called a Taylor polynomial. The Taylor series of a function is the limit of that function's Taylor polynomials, provided that the limit exists. A function may not be equal to its Taylor series, even if its Taylor series converges at every point. A function that is equal to its Taylor series in an open interval (or a disc in the complex plane) is known as an analytic function.
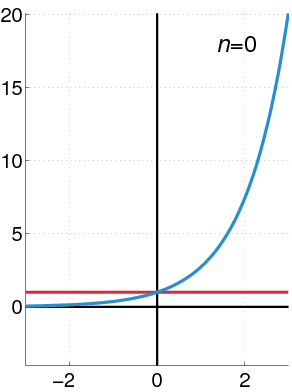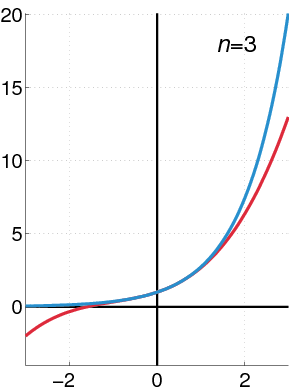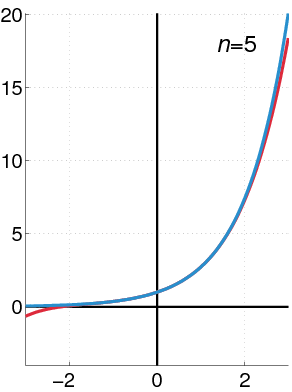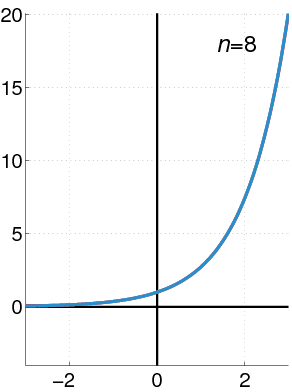
Exponential Function as a Power Series
The exponential function (in blue) and the sum of the first
The Taylor series of a real or complex-valued function
where
Example 1
The Maclaurin series for
so the Taylor series for
Example 2
The Taylor series for the exponential function