A sequence is an ordered list of objects (or events). Like a set, it contains members (also called elements, or terms). The number of ordered elements (possibly infinite) is called the length of the sequence. Unlike a set, order matters in a sequence, and exactly the same elements can appear multiple times at different positions in the sequence. Most precisely, a sequence can be defined as a function whose domain is a countable, totally ordered set, such as the natural numbers.
Examples:
Indexing
The terms of a sequence are commonly denoted by a single variable, say
This represents the sequence
Sequences can be indexed beginning and ending from any integer. The infinity symbol,
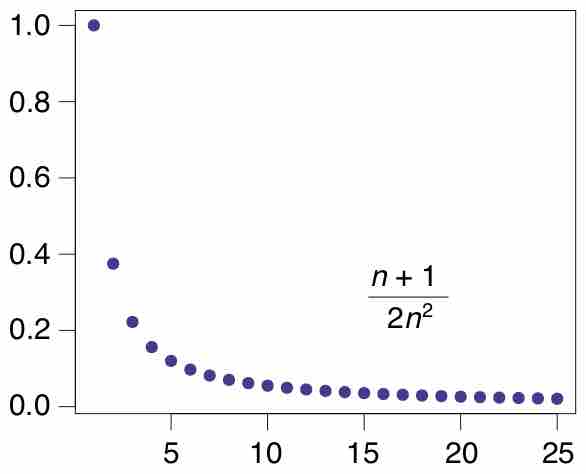
A Convergent Sequence
The plot of a convergent sequence (
Specifying a Sequence by Recursion
Sequences whose elements are related to the previous elements in a straightforward way are often specified using recursion. This is in contrast to the specification of sequence elements in terms of their position. To specify a sequence by recursion requires a rule to construct each consecutive element in terms of the ones before it. In addition, enough initial elements must be specified so that new elements of the sequence can be specified by the rule.
Example
The Fibonacci sequence can be defined using a recursive rule along with two initial elements. The rule is that each element is the sum of the previous two elements, and the first two elements are