A power series (in one variable) is an infinite series of the form:
where
can be written as a power series around the center
or, indeed, around any other center
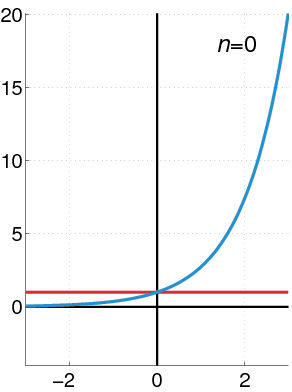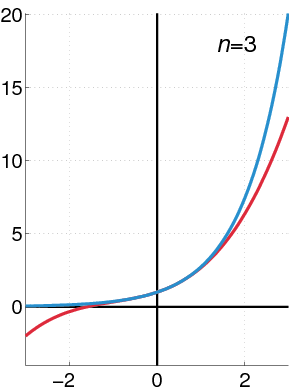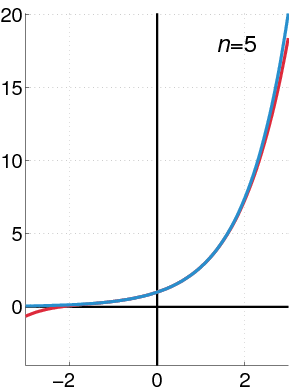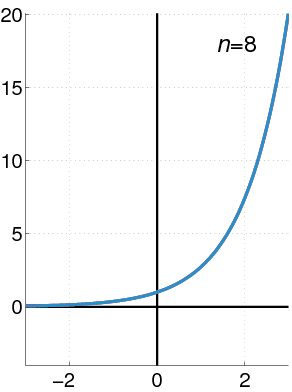
Exponential Function as a Power Series
The exponential function (in blue), and the sum of the first
In many situations
These power series arise primarily in real and complex analysis, but also occur in combinatorics (under the name of generating functions) and in electrical engineering (under the name of the
Radius of Convergence
A power series will converge for some values of the variable
if this limit exists.