Concept
Version 7
Created by Boundless
Comparison Tests
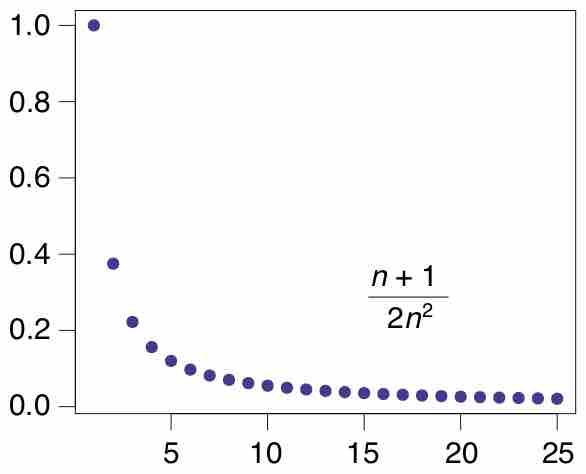
Limit Convergence Test
The ratio between
Source
Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources: