Trigonometric Functions and the Unit Circle
We have already defined the trigonometric functions in terms of right
triangles. In this section, we will redefine them in terms of the unit
circle. Recall that a unit circle is a circle centered at the origin
with radius 1. The angle
The x- and y-axes divide the coordinate plane (and the unit circle, since it is centered at the origin) into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, II, III, and IV.
For any angle
The diagram of the unit circle illustrates these coordinates.
Unit circle
Coordinates of a point on a unit circle where the central angle is
Note
that the values of
For an example of how this applies, consider the diagram showing the point with coordinates
Point on a unit circle
The point
We know that, for any point on a unit circle, the
Recall that
We have previously discussed trigonometric functions as they apply to right triangles. This allowed us to make observations about the angles and sides of right triangles, but these observations were limited to angles with measures less than
Further Consideration of the Unit Circle
The coordinates of certain points on the unit circle and the the measure of each angle in radians and degrees are shown in the unit circle coordinates diagram. This diagram allows one to make observations about each of these angles using trigonometric functions.
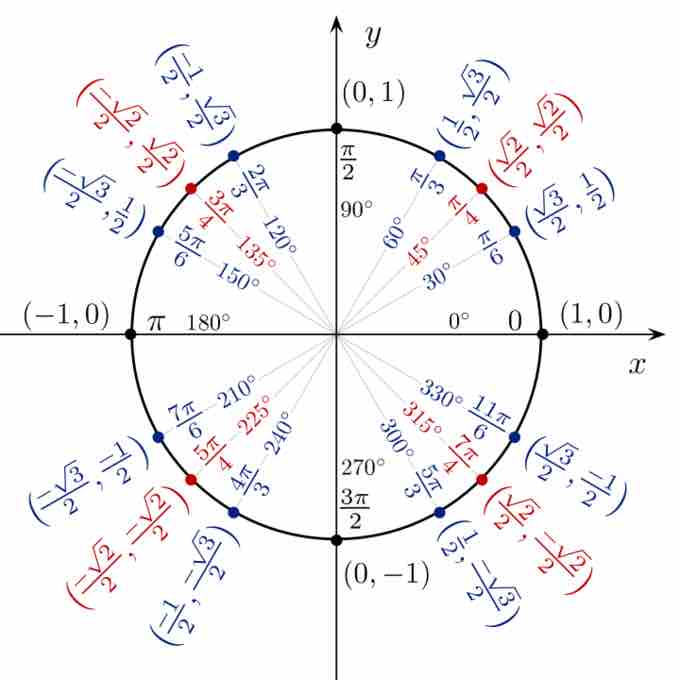
Unit circle coordinates
The unit circle, showing coordinates and angle measures of certain points.
We can find the coordinates of any point on the unit circle. Given any angle
The unit circle demonstrates the periodicity of trigonometric functions. Periodicity refers to the way trigonometric functions result in a repeated set of values at regular intervals. Take a look at the
We can identify a pattern in these numbers, which fluctuate between
Example
Solve
It seems like this would be complicated to work out. However, notice that the unit circle diagram shows the coordinates at