In mathematics, factorization (or factoring) is the process of breaking an object (such as a number or algebraic expression) down into a product of other objects, or factors, which when multiplied together give the original number or expression. The aim of factoring is to reduce something to "basic building blocks." This process has many real-life applications and can help us solve problems in mathematics.
In particular, factoring a number means to break it down into numbers that when multiplied back together produce the given number. For now, we will focus on factoring whole numbers.
For example, consider the number 24. To find the factors, consider the numbers that yield a product of 24. We know that
Prime Factorization
Prime factorization is a particular type of factorization that breaks a number of interest into prime numbers that when multiplied back together produce the original number. Such prime numbers are called prime factors.
Example 1
For example, consider the number 6. We know that
Example 2
Now, consider the number 12. We know that
Factor Trees and Prime Factorization
Every positive integer greater than 1 has a distinct prime factorization. To factor larger numbers, it can be helpful to draw a factor tree.
In a factor tree, the number of interest is written at the top. Then, two factors of that number are found and connected below that number with branches. This process repeats for each subsequent factor of the original number until all the factors at the bottoms of the branches are prime.
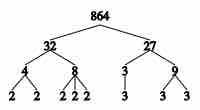
Prime factorization example
This factor tree shows the factorization of 864. It shows that 864 is the product of five 2s and three 3s. A shorthand way of writing these resulting prime factors is