Named for "the father of analytic geometry," 17th-century French mathematician René Descartes, the Cartesian coordinate system is a 2-dimensional plane with a horizontal axis and a vertical axis. Both axes extend to infinity, and arrows are used to indicate infinite length. The horizontal axis is known as the $x$-axis, and the vertical axis is known as the $y$-axis. The point where the axes intersect is known as the origin.

A Cartesian coordinate system is used to graph points. Points are specified uniquely in the Cartesian plane by a pair of numerical coordinates, which are the signed distances from the point to the two axes. Each point can be represented by an ordered pair $(x,y)$, where the $x$-coordinate is the point's distance from the $y$-axis and the $y$-coordinate is the distance from the $x$-axis. The origin where the two axes meet is therefore $(0,0)$. On the $x$-axis, numbers increase toward the right and decrease toward the left; on the $y$-axis, numbers increase going upward and decrease going downward.

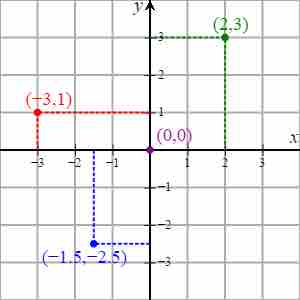
Cartesian coordinate system

The Cartesian coordinate system with 4 points plotted, including the origin, at $(0,0)$.

Plotting Points

To plot the point $(2,3)$, for example, you start at the origin (where the two axes intersect). Then, move three units to the right and two units up. 

 The point $(-3,1)$ is found by moving three units to the left of the origin and one unit up.

The non-integer coordinates $(-1.5,-2.5)$ lie between -1 and -2 on the $x$-axis and between -2 and -3 on the $y$-axis. Therefore, you move one and a half units left and two and a half units down.

Independent and Dependent Variables  

A Cartesian plane is particularly useful for plotting a series of points that show a relationship between two variables.

For example, there is a relationship between the number of cars a car wash cleans and the money the business makes (its revenue). The revenue, or output, depends upon the number of cars, or input, that they wash. Therefore, the revenue is the dependent variable ($y$), and the number of cars is the independent variable ($x$).  The revenue is plotted on the $y$-axis, and the number of cars washed is plotted on the $x$-axis.

Quadrants 

The Cartesian coordinate system is broken into four quadrants by the two axes. These quadrants are labeled I, II, III, and IV, starting from the upper right and continuing counter-clockwise, as pictured below.

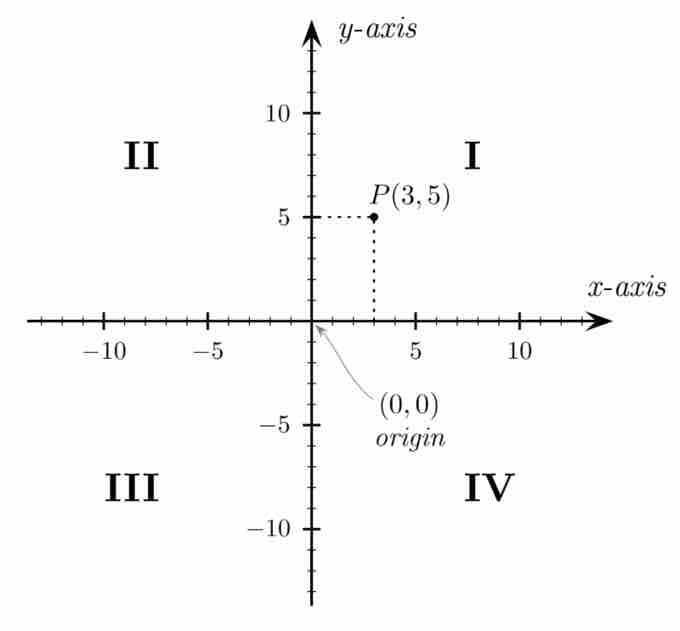
Cartesian coordinates

The four quadrants of theCartesian coordinate system. The arrows on the axes indicate that they extend infinitely in their respective directions.

Some basic rules about these quadrants can be helpful for quickly plotting points:

• Quadrant I: Points have positive $x$ and $y$ coordinates, $(x,y)$.
• Quadrant II: Points have negative $x$ and positive $y$ coordinates, $(-x,y)$.
• Quadrant III: Points have negative $x$ and $y$ coordinates, $(-x,-y)$.
• Quadrant IV: Points have positive $x$ and negative $y$ coordinates, $(x,-y)$.
• Points that have a value of 0 for either coordinate lie on the axes themselves and are not considered to be in any of the quadrants (e.g., $(4,0)$, $(0,-2)$).