Minima and maxima are used heavily in optimization problems and artificial intelligence where, given a number of constraints on resources, we want the best use of our resources. For instance, we may want to maximize our profits given the items we can make and our available resources. In artificial intelligence we may want to discover what the least costly plan of action to take is for a robot (ie. the shortest path). Ideally you'd want to find the global minima for the plans. However, because there is not unlimited time to identify the right plan, artificial intelligence often simply finds the local minima.
Definitions of Minimums and Maximums: Relative versus Global
In mathematics, the maximum and minimum of a function (known collectively as extrema) are the largest and smallest value that a function takes at a point either within a given neighborhood (local or relative extremum) or within the function domain in its entirety (global or absolute extremum).
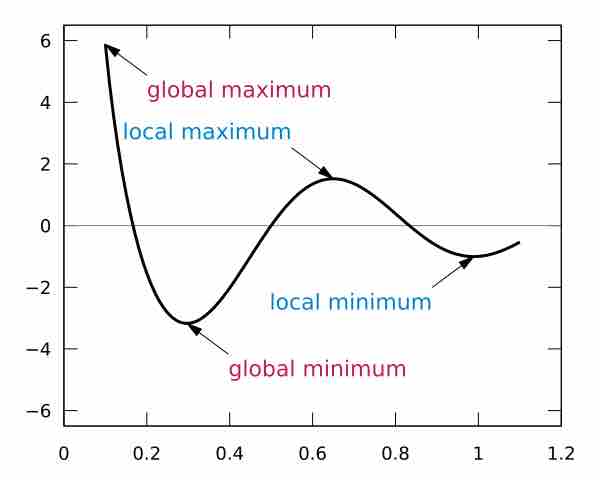
Examples of Relative and Global Extrema
This graph has examples of all four possibilities: relative (local) maximum and minimum, and global maximum and minimum.
While some functions are increasing (or decreasing) over their entire domain, many others are not. A value of the input where a function changes from increasing to decreasing (as we go from left to right, that is, as the input variable increases) is called a relative maximum. If a function has more than one, we say it has local maxima. Similarly, a value of the input where a function changes from decreasing to increasing as the input variable increases is called a relative minimum. The plural form is local minima.
A function is also neither increasing nor decreasing at extrema. Note that we have to speak of local extrema, because any given local extremum as defined here is not necessarily the highest maximum or lowest minimum in the function’s entire domain.
-
A function
$f$ has a relative (local) maximum at$x=b$ if there exists an interval$(a,c)$ with$a<b<c$ such that, for any$x$ in the interval$(a,c)$ ,$f(x)≤f(b)$ . - Likewise,
$f$ has a relative (local) minimum at$x=b$ if there exists an interval$(a,c)$ with$a<b<c$ such that, for any$x$ in the interval$(a,c)$ ,$f(x)≥f(b)$ .
Local Maximum Minimum Graph
For the function pictured, the local maximum is at the
A function has a global (or absolute) maximum point at
Functions may not have any extrema in them, such as the line
Distingushing Relative and Global Maximum and Minimum
Example 1: Find all maxima and minima in the graph below:
Relative Max and Min graph
This curve shows a relative minimum at
The graph attains a local maximum at
The graph attains a local minimum at
Example 2: Find all global maxima and minima in the graph below:
Global Max and Min Graph
For the function pictured above, the absolute maximum occurs twice at
The graph attains an absolute maximum in two locations,
The graph attains an absolute minimum at